Tutoriel maths : La distance entre deux points
Recommandés
La distance entre deux points ? C’est évident, mais le fondemnt mérite de lui prêter plus d’attention.
Dans un système de référence cartésien, il est possible de déterminer la distance entre deux points. Diverses situations peuvent se produire.
Sqrt est la méthode statique en lanage python pour la raciné carée
SEGMENTS HORIZONTAUX (avec le même cadre)
La distance entre deux points A et B ayant la même ordonnée est donnée par la valeur absolue de la différence entre les abscisses des deux points.
La valeur absolue est considérée car la mesure d’un segment ne peut jamais être négative.
Si on appelle x _ {{a}} et x _ {{b}} les abscisses des points on a : AB = | x _ {{a}} – x _ {{b}} |.
Par exemple, on calcule la longueur du segment AB dont les extrémités ont pour coordonnées : A (1 ; 2) B (5 ; 2) :
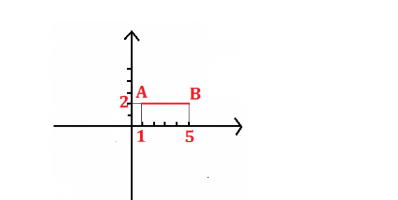
AB = | x _ {{a}} – x _ {{b}} | = | -1 – (- 5) | = -1 + 5 = + 4.
Vous pouvez aussi les inverser en faisant \ left \ | x _ {{b}} – x _ {{a}} \ droite \ | et le résultat sera toujours +4
Évidemment, la valeur du segment, parfois, peut également être vue à l’œil nu lorsque le graphique est dessiné sur une feuille quadrillée, puis les carrés pourraient être comptés pour connaître la longueur.
SEGMENTS VERTICAUX de même abscisse
La distance entre deux points A et B ayant la même abscisse est donnée par la valeur absolue de la différence entre les ordonnées des deux points.
AB = | y _ {{a}} – y _ {{b}} |.
La valeur absolue est considérée car un segment ne peut jamais être négatif.
On calcule la longueur du segment AB dont les extrémités ont pour coordonnées A (3 ; 2) et B (3 ; 1)
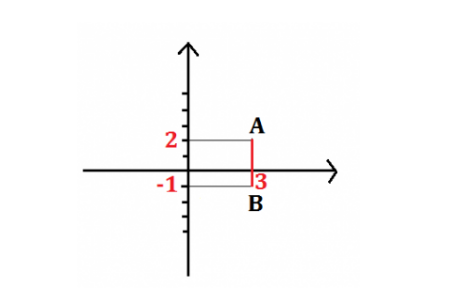
Sur le graphique on observe que la longueur du segment AB est de 3u.
On obtient le même résultat en appliquant la formule :
AB = | y _ {{a}} – y _ {{b}} | = | 2 – (- 1) | = | 2 + 1 | = + 3
Si vous deviez faire un segment vertical sur une feuille quadrillée où chaque unité est représentée par un petit carré, si nous étions en difficulté nous pourrions simplement compter les carrés d’un extrême à l’autre.
SEGMENTS OBLIQUES : DISTANCE ENTRE DEUX POINTS GÉNÉRIQUES
La mesure de la distance entre deux points est égale à la racine carrée de la somme des carrés des différences des abscisses et des ordonnées des points.
Soient A et B deux points ayant respectivement pour coordonnées les nombres x _ {{a}}, y _ {{a}} et x _ {{b}}, y _ {{b}} ; c’est-à-dire A (x _ {{a}}, y _ {{a}}) et B (x _ {{b}}, y _ {{b}}).
On indique avec A’ et B’ les projections de A et B sur l’axe des x on aura :
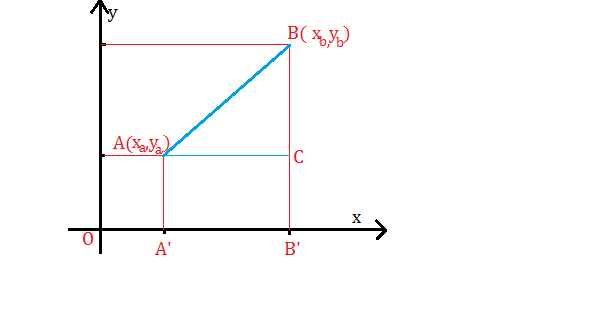
OB ‘= x _ {{b}} ; OA ‘= x _ {{a}} ; B’B = y _ {{b}} ; B’C =, y _ {{a}} alors :
AC = OB’-OA ‘= x_ {b} – x _ {{a}} ;
CB = B’B – B’C = y_ {b} – y _ {{a}}
En appliquant le théorème de Pythagore au triangle ABC, nous aurons :
AB = \ sqrt {AC ^ {2} + CB ^ {2}} =
\ sqrt {(x_ {b} -x_ {a}) ^ {2} + (y_ {b} -y_ {a}) ^ {2}}
EXEMPLE
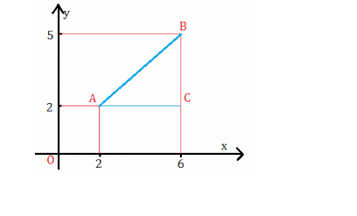
Calculez la mesure de distance des points A (2,2) et B (6,5).
On a:
AB = \ sqrt {(x _ {{b}} – x _ {{a}}) ^ {2} + (y _ {{b}} – y _ {{a}}) ^ {2}}
AB = \ carré {(6-2) ^ {2} + (5-2) ^ {2}} = \ carré {4 ^ {2} +3 ^ {2}} =
= \ sqrt {16 + 9} = \ sqrt {25} = 5.