Cours Algorithme : Initiation à la programmation

Ce cours élémentaire intitulé “Algorithme” vise à enseigner les principes fondamentaux de la programmation informatique.

Introduction à la programmation

Pour résoudre un problème informatique, l’utilisateur doit concevoir un programme qu’il exécute ensuite sur l’ordinateur. L’ordinateur, à son tour, traite les instructions du programme pour générer les résultats requis en fonction des données fournies. Un programme consiste en une séquence logique et organisée d’instructions, et la programmation englobe l’ensemble des activités nécessaires à la création d’un tel programme. Pour rédiger un programme, certaines étapes incontournables sont les suivantes :

• Bien connaître le problème.
• Savoir le découper logiquement en un ensembled’opérations élémentaires (actions).
• Connaître un langage compréhensible par la machine.

Objectif de l’algorithmique

L’objectif fondamental de l’algorithmique consiste à réaliser une analyse approfondie du problème en vue de présenter la solution optimale. Cette solution doit être à la fois exacte, rapide, précise et économique, en recourant à diverses techniques de programmation.

Il est essentiel de noter que, en informatique, l’étape d’analyse d’un problème peut représenter jusqu’à 90% du temps total alloué à la résolution de ce dernier. Cette phase d’analyse a pour but de :

Le processus algorithmique comprend deux étapes cruciales. La première consiste à traduire le texte du problème en une série d’étapes élémentaires, créant ainsi un schéma de résolution. La seconde étape implique la révision des outils élémentaires employés dans la solution, avec l’objectif d’optimiser le schéma autant que possible avant d’entamer la phase de programmation.

Il est important de noter que les erreurs les plus courantes lors de la résolution de problèmes informatiques se produisent lorsqu’un individu, après avoir défini les spécifications du projet, s’empresse de saisir un programme sans réfléchir en profondeur à l’analyse du problème. Cela peut être dû au fait que l’on ne maîtrise qu’un langage de programmation spécifique, conduisant ainsi à une tentative de solution (même complexe) en utilisant exclusivement les fonctionnalités de ce langage. Cependant, il est crucial de ne pas devenir captif d’un langage particulier. Il faut chercher la solution au problème de manière indépendante du langage de programmation.

Exemple :

Imaginons un problème de calcul complexe à résoudre. Plutôt que de se précipiter pour écrire un programme en utilisant uniquement les fonctions d’un langage de programmation familier, la méthode algorithmique suggère de d’abord décomposer le problème en étapes simples, puis d’examiner les meilleures approches possibles pour optimiser le processus avant de passer à la programmation proprement dite. Cela garantit une solution plus efficace et flexible, indépendamment du langage de programmation choisi.

Synthèse

Un algorithme se présente comme un processus de décomposition des étapes requises pour résoudre un problème donné. Ses caractéristiques essentielles incluent :

1. Inclure un nombre limité d’actions réalisables par une machine.
2. Solliciter uniquement des données que l’utilisateur connaît déjà.
3. Offrir des résultats significatifs pour l’utilisateur.
4. Être exécutable manuellement par une personne, utilisant des moyens tels qu’un stylo et du papier, sans nécessiter d’ordinateur ou de dispositif électronique.

Exemple : Prenons le problème de la multiplication de deux nombres. Un algorithme simple pourrait consister en ces étapes :

1. Demandez à l’utilisateur de fournir deux nombres.
2. Multipliez ces deux nombres ensemble.
3. Affichez le résultat de la multiplication à l’utilisateur.

Cet algorithme suit les principes énoncés, car il comporte un nombre limité d’actions (trois étapes), n’utilise que des données que l’utilisateur connaît (les deux nombres fournis), génère un résultat pertinent (le produit des deux nombres), et peut être exécuté manuellement avec un stylo et du papier.

• L’analyse d’un problème complexe peut parfois nous conduire à le décomposer en sous-problèmes que nous résolvons individuellement, sans tenir compte des éventuelles interactions entre les solutions, ce qui peut aboutir à une solution globale incorrecte.
• En général, pour résoudre un problème, on tend à produire une solution fonctionnelle, mais qui peut être complexe, difficile à lire, et exiger beaucoup de temps d’exécution et d’espace mémoire.

Définition d’un algorithme

Un algorithme se compose d’un ensemble fini d’étapes, chaque étape étant formée d’un ensemble fini d’opérations dont chacune est définie d’une façon rigoureuse (sans ambiguïté).
Cet environnement est constitué :

• des objets d’entrée (OE) qui représentent l’ensemble de données que l’utilisateur doit introduire à l’algorithme,
  
• des objets de sortie (OS) qui représentent l’ensemble des résultats produits par l’algorithme,
  
• des objets constants (OC) qui représentent l’ensemble des objets dont les valeurs ne changent pas au cours de toute
  l’exécution de l’algorithme,
  
• des objets intermédiaires (OI) qui représentent l’ensemble des objets de traitements internes, ils ne sont
  ni entrés ni sortis, mais ils sont soit des compteurs, soit calculés à partir des objets d’entrée et des objets constants et serviront pour produire les objets de sortie.

Exemple 1 : calcul de la quantité Q donnée par la formule suivante :

Q= a- b /2.c +b

Proposition d’une méthode de révolution

Voici les étapes de la méthode : Si certains sous-problèmes semblent encore trop complexes, il est recommandé de les décomposer davantage en sous-sous-problèmes. En fin de compte, la résolution du problème initial consiste à résoudre tous ces sous-problèmes issus des diverses décompositions. Avant de commencer la résolution, la première question à se poser est :

Qu’est-ce que cet algorithme doit produire comme résultats ?

C’est-à-dire demander au client quels sont les objets de sortie de notre algorithme.

Chacun de ces objets va constituer une racine d’un arbre imaginé horizontal de la droite vers la gauche.

• On se dirige vers la gauche en posant, pour chaque objet, les
questions suivantes:
• L’objet se calcule? si oui en fonction de quoi ?
• Sinon, l’objet est constant? si oui quelle est sa valeur  ?
Sinon, il ne peut être qu’une donnée du problème, c’est- à-dire un objet d’entrée.

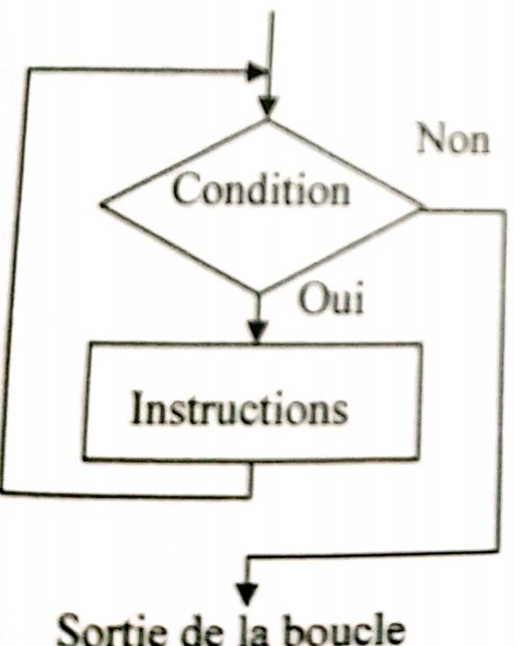
Ce raisonnement est expliqué par le schéma suivant :

On utilise ce raisonnement pour tous les éléments de l’environnement jusqu’à atteindre les “extrémités de la branche”, qui sont généralement soit des éléments constants, soit des éléments d’entrée du problème.

Application

Appliquons la méthode citée ci-dessus pour le problème de calcul de la quantité Q (définie ci-dessus dansl’exemple 1).
Notre algorithme doit calculer la quantité Q.

Ce problème paraît compliqué car il consiste en trois opérations combinées. Pour le simplifier, on propose
d’écrire : 
N=a-b
E=F.c
D=E+b
Donc :
Q =  N / D

Q se calcule en fonction de N et D.
Reprenons le même raisonnement pour :
N qui se calcule en fonction de a et b
D qui se calcule en fonction de E et b
E qui se calcule en fonction de c et F

Qu’est-ce qu’un bon algorithme ?

On peut noter qu’un bon algorithme est un schéma de résolution possédant

les caractéristiques suivantes :

• Correct : s’il répond au problème posé
• Précis : s’il fournit exactement les résultats attendus
• Rapide : s’il utilise un temps d’exécution minimal indépendamment de la vitesse de la machine
• Efficace : s’il utilise le moins d’espace mémoire possible
• Clair et lisible : s’il ne présente pas de difficulté de compréhension pour un autre programmeur désirant le
• maintenir ou le développer
• Résistant : s’il est capable de détecter les cas de mauvaises utilisations.

Exemple 2 : résistance d’un algorithme
Dans la résolution d’une équation de premier degré :
a.x +b = 0
Pour laquelle :
x = -b /a

Un algorithme de résolution de cette équation doit réagir si on lui introduit une valeur a = 0 (mauvaise utilisation), en efusant de calculer la solution et en affichant par conséquent un message d’erreur, sinon la machine va se bloquer car elle ne sait pas faire des divisions par zéro.

Conclusion

Un algorithme est constitué :
– d’un ensemble d’objets appelé environnement de l’algorithme?

– d’un ensemble d’actions agissant sur cet environnement.

Exemple 3 : algorithme de calcul de la somme de deux nombres réels

Analyse du problème :

Objets d’entrée (OE) : A,B

Objets de sortie (OS) :S

Formule :S= A +B

Remarque : dans une analyse, il se peut qu’on ne trouve pas
tous les quatre types d’objets de l’environnement (OE), (OS), (OI) et (OC).