Calcul de la VAN avec Cash Flow Constant – Exercices Corrigés

Q: Quand peut-on utiliser la formule d’annuité pour calculer la VAN

On l’utilise lorsque le cash-flow net est identique à chaque période et que les périodes sont régulières. Formule : VAN = -I0 + CF × (1 - (1 + r)^(-n)) / r.

Q: Comment interpréter une VAN positive, nulle ou négative

VAN > 0 : création de valeur au taux r. VAN = 0 : équilibre. VAN < 0 : destruction de valeur, projet à corriger ou écarter.

Q: Quel est le piège le plus fréquent sur le taux d’actualisation

Mélanger les unités de temps : taux annuel avec flux mensuels (ou inversement). CF, r et n doivent avoir la même périodicité.

Q: Comment vérifier rapidement que le résultat est cohérent

Si r augmente, la VAN baisse généralement. Si CF augmente, la VAN augmente. Si n augmente, la VAN tend à augmenter mais l’effet diminue avec le temps.

La VAN avec cash-flow constant permet d’évaluer rapidement la rentabilité d’un projet lorsque les flux nets restent identiques à chaque période. Le calcul consiste à actualiser une série de cash-flows réguliers, puis à comparer leur valeur actuelle à l’investissement initial pour conclure sur la création de valeur. Les exercices corrigés structurent la méthode, sécurisent le choix du taux d’actualisation et entraînent à interpréter correctement une VAN positive, nulle ou négative selon les hypothèses retenues.

Calculer la VAN avec cash-flow constant et réussir les exercices corrigés

La Valeur Actuelle Nette (VAN) est un indicateur financier utilisé pour évaluer la rentabilité d’un projet d’investissement en actualisant les flux de trésorerie futurs. Lorsque les flux de trésorerie sont constants (identiques chaque année), la formule de la VAN devient plus simple à appliquer.

Méthode

VAN avec cash-flow constant : calcul rapide + schémas

1) Identifier les données I0 • CF • r • n

I0 : investissement initial (sortie de cash, généralement négative)
CF : cash-flow net constant par période (même montant chaque année/mois)
r : taux d’actualisation (coût du capital / exigence de rendement)
n : nombre de périodes

2) Schéma des flux (chronologie)

t=0 t=1 t=2 t=3 … t=n |———-|———-|———-|———-|———-| -I0 +CF +CF +CF … +CF

3) Actualiser les flux et calculer la VAN

VAN = -I0 + Σ ( CF / (1 + r)^t ) pour t = 1 → n

4) Formule « annuité » (cas cash-flow constant)

Quand CF est identique à chaque période, on utilise la valeur actuelle d’une annuité :

VA(annuité) = CF × [ (1 – (1 + r)^(-n)) / r ]

VAN = -I0 + CF × [ (1 – (1 + r)^(-n)) / r ]

Lecture : la partie entre crochets est un coefficient qui transforme un CF constant en valeur actuelle.

Schéma « filtre » de décision

Calcul VAN | v VAN > 0 → Projet créateur de valeur (à retenir) VAN = 0 → Projet à l’équilibre (décision selon stratégie/risque) VAN < 0 → Projet destructeur de valeur (à corriger/écarter)

Schéma de sensibilité (r influence la VAN)

Taux r ↑ → Actualisation plus forte → VA des CF ↓ → VAN ↓ Taux r ↓ → Actualisation plus faible → VA des CF ↑ → VAN ↑

Mini check-list anti-erreurs

Le CF est bien net (encaissements − décaissements).
La période est cohérente : r annuel avec CF annuels, r mensuel avec CF mensuels.
I0 est placé en t=0 (pas en t=1).
La VAN se lit avec le même r que celui exigé par l’entreprise.

Piège fréquent : utiliser un taux annuel avec des flux mensuels (ou inversement) fausse totalement la VAN.

1. Formule de la VAN avec Flux de Trésorerie Constant

La formule générale pour calculer la VAN avec des flux de trésorerie constants est la suivante :

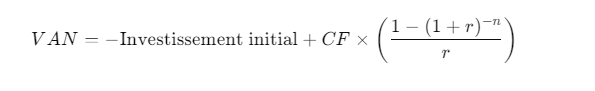
Où :

CF : montant du flux de trésorerie constant (cash flow annuel)
r : taux d’actualisation
n : durée du projet (en années)
Investissement initial : montant investi au début du projet

2. Exemple d’Application

Énoncé

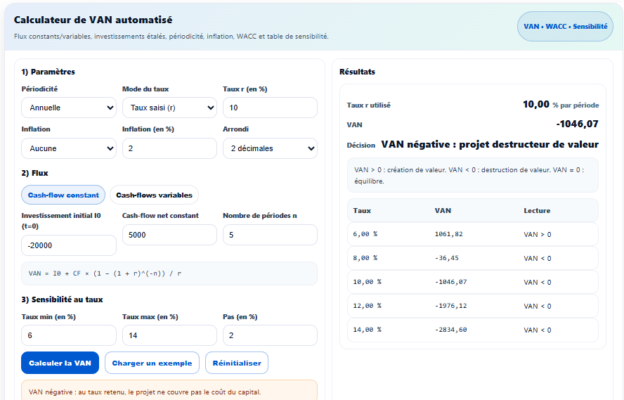
Une entreprise investit 20 000 € dans un projet qui génère un flux de trésorerie constant de 5 000 € chaque année pendant 5 ans. Le taux d’actualisation est de 10 %. Calculez la VAN du projet.

Solution

1. Données

Investissement_initial: 20000
Cash_flow_annuel: 5000
Taux_actualisation: 0.10
Nombre_annees: 5

2. Application de la Formule

La formule de la VAN est :

Formule VAN (cash-flow constant)

VAN = -20 000 + 5 000 × ( (1 – (1 + 0.10)-5) / 0.10 )

3. Calcul des Éléments

Actualisation des flux constants :

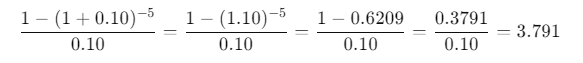
Calcul final :

VAN = – 20000 + 5000 * 3.791 = – 20000 + 18955 = – 1045 €

La VAN est de -1 045 €, ce qui signifie que le projet n’est pas rentable avec un taux d’actualisation de 10 %.

3. Exercice 1 : VAN avec Flux Constant Positif

Énoncé

Un projet nécessite un investissement initial de 10 000 € et génère un flux de trésorerie constant de 2 500 € chaque année pendant 6 ans. Le taux d’actualisation est de 8 %. Calculez la VAN du projet.

Solution

1. Données

Investissement_initial: 10000
Cash_flow_annuel: 2500
Taux_actualisation: 0.08
Nombre_annees: 6

2. Application de la Formule

La formule de la VAN est :

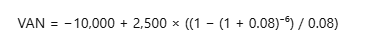
3. Calcul des Éléments

Actualisation des flux constants :

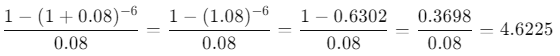
Calcul final :

VAN = – 10000 + 2500 * 4.6225 = – 10000 + 11556.25 = 1556.25 €

La VAN est de 1 556,25 €, ce qui signifie que le projet est rentable avec un taux d’actualisation de 8 %.

4. Exercice 2 : VAN avec Taux d’Actualisation Elevé

Énoncé

Une entreprise investit 50 000 € dans un projet qui génère un flux de trésorerie constant de 12 000 € par an pendant 7 ans. Le taux d’actualisation est de 12 %. Calculez la VAN du projet.

Solution

1. Données

Investissement_initial: 50000
Cash_flow_annuel: 12000
Taux_actualisation: 0.12
Nombre_annees: 7

2. Application de la Formule

La formule de la VAN est :

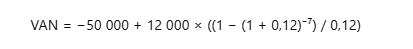
3. Calcul des Éléments

Actualisation des flux constants :

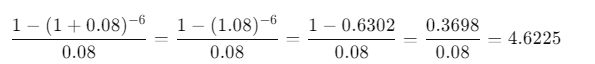
Calcul final :
VAN = – 50000 + 12000 * 4.5642 = – 50000 + 54770.4 = 4770.4 €

La VAN est de 4 770,40 €, ce qui signifie que le projet est rentable.

5. Exercice 3 : VAN avec Cash Flow Constant Négatif

Énoncé

Un projet nécessite un investissement initial de 15 000 € et génère un flux de trésorerie constant de -3 000 € (perte annuelle) pendant 5 ans. Le taux d’actualisation est de 10 %. Calculez la VAN.

Solution

1. Données

Investissement_initial: 15000
Cash_flow_annuel: -3000
Taux_actualisation: 0.10
Nombre_annees: 5

2. Application de la Formule

La formule de la VAN est :

Formule VAN (cash-flow constant négatif)

VAN = -15 000 – 3 000 ×
( (1 – (1 + 0.10)-5) / 0.10 )

3. Calcul des Éléments

Actualisation des flux constants :

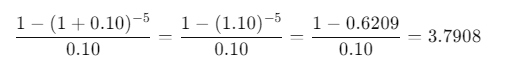
Calcul final :

VAN = – 15000 + (-3000) * 3.7908 = – 15000 – 11372.40 = – 26372.40 €

La VAN est de -26 372,40 €, ce qui signifie que le projet n’est pas rentable car les flux de trésorerie sont négatifs et ne permettent pas de récupérer l’investissement initial.

Le calcul de la VAN avec des flux de trésorerie constants est simplifié par la nature répétitive des flux, permettant l’utilisation d’une formule spécifique qui actualise ces flux sur la durée du projet. La VAN positive indique que le projet est rentable, tandis qu’une VAN négative signale une perte potentielle. Ces exercices permettent de voir comment ajuster et utiliser cette méthode pour des cas variés, allant des flux positifs à des flux négatifs et des projets avec des taux d’actualisation différents.

guide pratique pour calculer la VAN étape par étape

FAQ

VAN avec cash-flow constant : 4 questions pratiques

QQuand peut-on utiliser la formule d’annuité pour calculer la VAN

La formule d’annuité s’utilise quand le cash-flow net est identique à chaque période (même montant) et que les périodes sont régulières (années, mois).

VAN = −I0 + CF × (1 − (1 + r)^−n) / r

QComment interpréter une VAN positive, nulle ou négative

VAN > 0 : le projet crée de la valeur au taux r (décision favorable).
VAN = 0 : projet à l’équilibre (choix selon stratégie et contraintes).
VAN < 0 : le projet détruit de la valeur (à corriger ou écarter).

QQuel est le piège le plus fréquent sur le taux d’actualisation

Le piège classique est de mélanger les unités de temps : taux annuel avec flux mensuels (ou l’inverse).

Règle : CF, r et n doivent avoir la même périodicité.

QComment vérifier rapidement que le résultat est cohérent

Si r augmente, la VAN doit généralement baisser (actualisation plus forte).
Si CF augmente, la VAN doit augmenter.
Si n augmente, la VAN tend à augmenter, mais l’effet diminue au fil des périodes.