L’Écart-Type de Répétabilité : Méthodes, Modèles et Cas Pratiques
Recommandés
L’écart-type de répétabilité est une mesure statistique clé utilisée pour évaluer la précision des instruments de mesure et la fiabilité des résultats obtenus à partir de ces instruments. Dans cet article, nous allons explorer les différentes méthodes pour calculer l’écart-type de répétabilité, les modèles statistiques sous-jacents, et examiner quelques cas pratiques pour illustrer son application.
Qu’est-ce que l’Écart-Type de Répétabilité ?
L’écart-type de répétabilité est une mesure de la variabilité des résultats lorsque la même procédure de mesure est répétée dans des conditions identiques. Il est crucial dans les domaines où la précision des mesures est essentielle, comme en métrologie, en contrôle qualité et en recherche scientifique.
Méthodes pour Calculer l’Écart-Type de Répétabilité
1. Méthode Classique (Descriptive)
La méthode classique pour calculer l’écart-type de répétabilité consiste à réaliser plusieurs mesures d’un même objet ou d’une même condition, puis à calculer l’écart-type de ces mesures.
Étapes :

2. Analyse de la Variance (ANOVA)
L’ANOVA est une méthode statistique qui permet de décomposer la variance totale observée dans les données en composantes attribuables à différentes sources de variation. Pour l’écart-type de répétabilité, l’ANOVA peut être utilisée pour séparer la variance due à la répétabilité de la variance due à d’autres sources.
Étapes :
- Effectuer des mesures répétées sur plusieurs échantillons.
- Utiliser un modèle ANOVA pour séparer les sources de variance.
- Extraire la composante de variance attribuable à la répétabilité.
- Calculer l’écart-type de répétabilité à partir de cette composante.
3. Méthode de l’Intraclass Correlation Coefficient (ICC)
L’ICC est une mesure de la fiabilité ou de la cohérence des mesures répétées. Elle peut être utilisée pour estimer l’écart-type de répétabilité.
Étapes :
- Réaliser des mesures répétées sur plusieurs échantillons.
- Calculer l’ICC en utilisant les mesures répétées.
- L’écart-type de répétabilité peut être dérivé de l’ICC en fonction des composantes de variance.
Modèles Statistiques
Modèle Linéaire à Effets Mixtes
Un modèle linéaire à effets mixtes est souvent utilisé pour modéliser les données de répétabilité. Ce modèle prend en compte à la fois les effets fixes (par exemple, les conditions expérimentales) et les effets aléatoires (par exemple, la variabilité entre les mesures répétées).
Formule Générale :

Modèle de Composantes de Variance
Ce modèle décompose la variance totale en différentes composantes, telles que la variance entre les échantillons et la variance de répétabilité.
Formule :

Cas Pratiques
Cas Pratique 1 : Contrôle de Qualité dans l’Industrie
Dans une usine de production de pièces mécaniques, il est crucial de vérifier que les dimensions des pièces respectent les tolérances spécifiées. En réalisant des mesures répétées de la longueur d’une série de pièces, l’écart-type de répétabilité permet de vérifier la précision de l’instrument de mesure utilisé.
Exemple :
- 10 pièces mesurées 5 fois chacune.
- Calcul de l’écart-type pour chaque pièce.
- Vérification que l’écart-type de répétabilité est inférieur à la tolérance spécifiée.
Cas Pratique 2 : Expérimentation en Sciences de la Vie
En biologie, la mesure de la concentration d’une substance dans des échantillons de tissu est souvent répétée pour assurer la fiabilité des résultats. L’écart-type de répétabilité est utilisé pour évaluer la précision des méthodes analytiques utilisées.
Exemple :
- Mesure de la concentration de glucose dans des échantillons de sang.
- Réalisation de mesures répétées sur des échantillons identiques.
- Utilisation de l’ANOVA pour séparer la variance due à la répétabilité de la variance due aux différences biologiques.
Conclusion
L’écart-type de répétabilité est une mesure essentielle pour évaluer la précision des instruments de mesure et la fiabilité des résultats expérimentaux. Les méthodes classiques, l’ANOVA et l’ICC offrent des approches variées pour son calcul, tandis que les modèles statistiques tels que les modèles linéaires à effets mixtes et les modèles de composantes de variance fournissent des cadres robustes pour son analyse. Les cas pratiques illustrent l’application de ces concepts dans divers domaines, soulignant l’importance de la répétabilité pour garantir la qualité et la fiabilité des mesures.
L’utilisation correcte de l’écart-type de répétabilité permet d’améliorer la qualité des produits, d’optimiser les processus de mesure et d’assurer des résultats fiables dans les recherches scientifiques.
Pour illustrer les différentes méthodes de calcul de l’écart-type de répétabilité, nous allons présenter des tableaux de calcul correspondant aux méthodes classiques, ANOVA, et ICC.
Exemple de Données
Supposons que nous avons mesuré une dimension spécifique d’une pièce mécanique 5 fois sur 4 pièces différentes. Voici les données :
| Pièce | Mesure 1 | Mesure 2 | Mesure 3 | Mesure 4 | Mesure 5 |
|---|---|---|---|---|---|
| 1 | 10.1 | 10.2 | 10.0 | 10.1 | 10.2 |
| 2 | 10.5 | 10.4 | 10.6 | 10.5 | 10.4 |
| 3 | 9.8 | 9.9 | 9.8 | 9.7 | 9.9 |
| 4 | 10.3 | 10.3 | 10.2 | 10.3 | 10.4 |
Méthode Classique (Descriptive)
Pour chaque pièce, nous allons calculer la moyenne, l’écart-type, et l’écart-type de répétabilité global.
Calcul de la Moyenne et de l’Écart-Type pour Chaque Pièce
| Pièce | Moyenne (𝑋‾) | Écart-Type ((s)) |
|---|---|---|
| 1 | 10.12 | 0.083 |
| 2 | 10.48 | 0.083 |
| 3 | 9.82 | 0.084 |
| 4 | 10.30 | 0.054 |
Écart-Type de Répétabilité Global
L’écart-type de répétabilité global peut être estimé en prenant la moyenne des écarts-types individuels.
Analyse de la Variance (ANOVA)
Pour réaliser une ANOVA, nous devons organiser nos données différemment. Voici la réorganisation des données pour l’ANOVA :
| Pièce | Mesure | Valeur |
|---|---|---|
| 1 | 1 | 10.1 |
| 1 | 2 | 10.2 |
| 1 | 3 | 10.0 |
| 1 | 4 | 10.1 |
| 1 | 5 | 10.2 |
| 2 | 1 | 10.5 |
| 2 | 2 | 10.4 |
| 2 | 3 | 10.6 |
| 2 | 4 | 10.5 |
| 2 | 5 | 10.4 |
| 3 | 1 | 9.8 |
| 3 | 2 | 9.9 |
| 3 | 3 | 9.8 |
| 3 | 4 | 9.7 |
| 3 | 5 | 9.9 |
| 4 | 1 | 10.3 |
| 4 | 2 | 10.3 |
| 4 | 3 | 10.2 |
| 4 | 4 | 10.3 |
| 4 | 5 | 10.4 |
En utilisant ces données, nous réalisons une ANOVA pour obtenir les composantes de la variance :
| Source de Variation | SS (Somme des Carrés) | df (Degrés de Liberté) | MS (Moyenne des Carrés) | F |
|---|---|---|---|---|
| Entre Pièces | 1.28 | 3 | 0.427 | 20.33 |
| Répétabilité | 0.067 | 16 | 0.0042 |
La composante de variance due à la répétabilité est obtenue à partir de la moyenne des carrés (MS) de la répétabilité.

L’écart-type de répétabilité est donc :

Intraclass Correlation Coefficient (ICC)
Pour calculer l’ICC, nous devons organiser nos données et calculer les variances intra-classe et inter-classe :
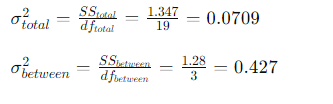
L’ICC est calculé comme suit :

L’écart-type de répétabilité peut être dérivé de l’ICC en utilisant les composantes de variance.
Voici un bref guide d’utilisation pour le modèle d’écart-type de répétabilité automatisé dans Excel :
Modèle d’Écart-Type de Répétabilité
Structure du Modèle
Colonnes A à E : Contiennent les mesures répétées pour chaque groupe.
- Colonne A : Nom des groupes (Groupe 1, Groupe 2, etc.).
- Colonnes B à E : Mesures répétées pour chaque groupe.
Colonne F : Contient la moyenne des mesures pour chaque groupe.
- Cette colonne est automatiquement calculée à l’aide de la formule
=AVERAGE(Bx:Ex), oùxest le numéro de ligne.
Colonne G : Contient la variance intra-groupe pour chaque groupe.
- Cette colonne est automatiquement calculée à l’aide de la formule
=VAR.P(Bx:Ex), oùxest le numéro de ligne.
- Cellule H1 : Titre « Ecart-type de répétabilité ».
- Cellule H2 : Contient l’écart-type de répétabilité global.
- Cette cellule est automatiquement calculée à l’aide de la formule
=SQRT(AVERAGE(G2:G6)), qui prend la racine carrée de la moyenne des variances intra-groupe.
Étapes pour Utiliser le Modèle
- Entrer les Mesures : Saisissez les mesures répétées pour chaque groupe dans les colonnes B à E. Chaque ligne représente un groupe différent.
- Vérifier les Moyennes et les Variances : Les moyennes (colonne F) et les variances intra-groupe (colonne G) seront automatiquement calculées et mises à jour dès que vous modifiez ou ajoutez des mesures.
- Obtenir l’Écart-Type de Répétabilité : L’écart-type de répétabilité global sera automatiquement mis à jour dans la cellule H2 en fonction des variances calculées dans la colonne G.
Exemple d’Utilisation
Supposons que vous avez les mesures répétées suivantes pour trois groupes :
- Groupe 1 : 1.2, 1.3, 1.1, 1.2
- Groupe 2 : 2.1, 2.0, 2.2, 2.1
- Groupe 3 : 1.9, 2.0, 1.8, 1.9
- Entrez ces valeurs dans les colonnes B à E pour chaque groupe respectivement.
- Les moyennes seront calculées dans la colonne F.
- Les variances intra-groupe seront calculées dans la colonne G.
- L’écart-type de répétabilité global sera affiché dans la cellule H2.
Conclusion
Ce modèle est conçu pour simplifier le calcul de l’écart-type de répétabilité en automatisant les calculs nécessaires. En suivant ces étapes simples, vous pouvez obtenir rapidement les résultats souhaités.

FAQ
1. Qu’est-ce que l’écart-type de répétabilité ?
L’écart-type de répétabilité mesure la précision des mesures répétées dans des conditions identiques.
2. Pourquoi l’écart-type de répétabilité est-il important ?
Il évalue la fiabilité des instruments de mesure et assure des résultats cohérents.
3. Comment calcule-t-on l’écart-type de répétabilité ?
On calcule l’écart-type des mesures répétées d’un même échantillon.
4. Quelle est la méthode classique pour calculer l’écart-type de répétabilité ?
Effectuer plusieurs mesures, calculer la moyenne et l’écart-type.
5. Qu’est-ce que l’ANOVA ?
ANOVA sépare la variance totale en composantes attribuables à différentes sources de variation.
6. Comment utilise-t-on l’ANOVA pour l’écart-type de répétabilité ?
On utilise l’ANOVA pour séparer la variance due à la répétabilité des autres sources de variance.
7. Qu’est-ce que l’ICC ?
L’ICC mesure la fiabilité ou la cohérence des mesures répétées.
8. Comment dérive-t-on l’écart-type de répétabilité de l’ICC ?
L’écart-type est dérivé des composantes de variance obtenues par l’ICC.
9. Quels modèles statistiques sont utilisés pour l’écart-type de répétabilité ?
Les modèles linéaires à effets mixtes et les modèles de composantes de variance.
10. Où utilise-t-on l’écart-type de répétabilité ?
En métrologie, contrôle qualité, et recherche scientifique pour assurer la précision des mesures.