Créer une Matrice de Corrélation en Python et Applications
Dans cet article, nous allons voir comment créer une matrice de corrélation en Python et explorer quelques applications pratiques.
💡 La corrélation est une mesure statistique qui exprime la force et la direction de la relation entre deux variables. Une matrice de corrélation est une table montrant les coefficients de corrélation entre plusieurs variables. Cette matrice est très utile en analyse de données et en machine learning pour comprendre les relations entre les variables.
Étape 1: Importer les Bibliothèques Nécessaires
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as pltNous utiliserons pandas pour la manipulation des données, numpy pour les opérations mathématiques, seaborn pour la visualisation, et matplotlib pour afficher les graphiques.
Étape 2: Charger les Données
Pour illustrer cet exemple, nous utiliserons le jeu de données Titanic de Kaggle. Vous pouvez charger vos propres données en remplaçant le chemin du fichier.
# Charger les données
df = pd.read_csv('titanic.csv')Étape 3: Sélectionner les Variables d’Intérêt
Nous devons sélectionner les variables numériques pour créer la matrice de corrélation, car la corrélation ne peut pas être calculée directement sur des variables catégorielles.
# Sélectionner les variables numériques
numeric_df = df.select_dtypes(include=[np.number])Étape 4: Calculer la Matrice de Corrélation
Utilisons la fonction corr de pandas pour calculer la matrice de corrélation.
# Calculer la matrice de corrélation
correlation_matrix = numeric_df.corr()
print(correlation_matrix)Étape 5: Visualiser la Matrice de Corrélation
Pour une meilleure compréhension, nous pouvons visualiser la matrice de corrélation avec un heatmap de seaborn.
# Visualiser la matrice de corrélation
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', linewidths=0.5)
plt.title('Matrice de Corrélation')
plt.show()Applications de la Matrice de Corrélation
1. Sélection de Fonctionnalités
En machine learning, la matrice de corrélation est souvent utilisée pour sélectionner les fonctionnalités. Des variables très corrélées peuvent redondantes, donc nous pourrions vouloir en supprimer certaines pour simplifier le modèle.
2. Détection des Multicolinéarités
La multicolinéarité se produit lorsque deux ou plusieurs variables indépendantes sont fortement corrélées entre elles. Cela peut poser des problèmes dans les modèles de régression. La matrice de corrélation aide à identifier ces relations.
3. Analyse Exploratoire des Données (EDA)
Avant de construire des modèles, il est crucial de comprendre les relations entre les variables. La matrice de corrélation fournit une vue d’ensemble des relations linéaires dans les données.
4. Identification des Relations Linéaires
Dans la recherche scientifique et les études de marché, la corrélation aide à identifier les relations linéaires potentielles entre les variables, ce qui peut orienter les hypothèses et les analyses ultérieures.
Études de Cas et Applications de la Matrice de Corrélation en Python
Pour illustrer l’utilité de la matrice de corrélation dans des contextes réels, examinons quelques études de cas dans différents domaines.
Étude de Cas 1: Analyse du Marché Boursier
Contexte
Un analyste financier souhaite examiner la relation entre plusieurs actions pour diversifier un portefeuille d’investissements. La matrice de corrélation peut aider à identifier les actions qui ont des relations faibles ou négatives entre elles, réduisant ainsi le risque global du portefeuille.
Données
Les données proviennent de plusieurs indices boursiers, comme les prix de clôture quotidiens des actions.
Code et Analyse
# Charger les données de prix de clôture des actions
stock_data = pd.read_csv('stock_prices.csv', index_col='Date', parse_dates=True)
# Calculer la matrice de corrélation
correlation_matrix = stock_data.corr()
# Visualiser la matrice de corrélation
plt.figure(figsize=(14, 10))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', linewidths=0.5)
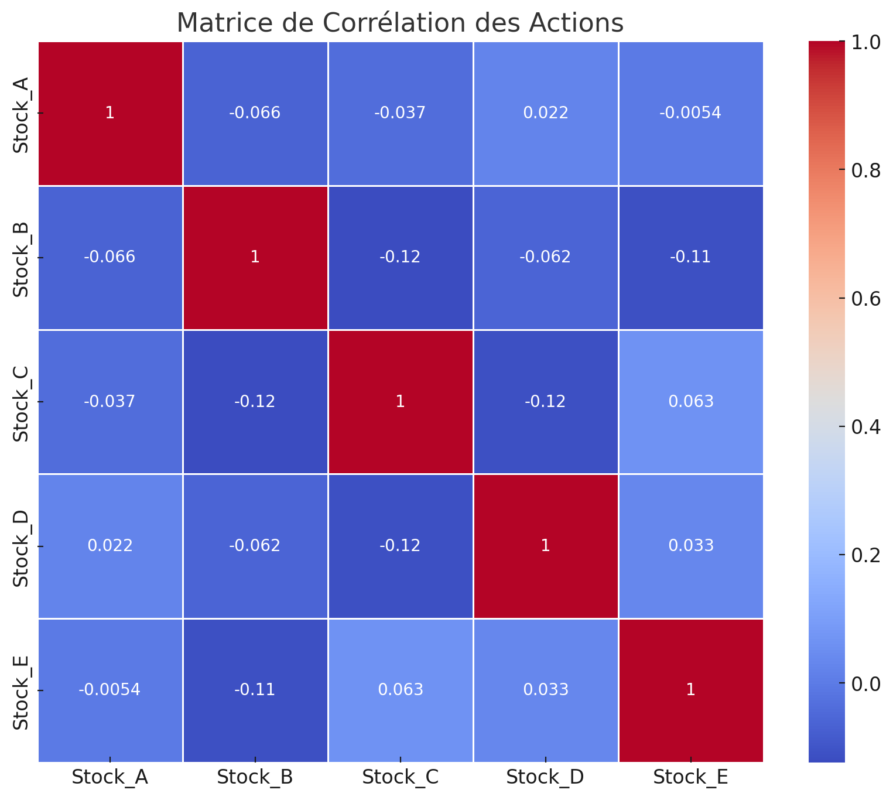
plt.title('Matrice de Corrélation des Actions')
plt.show()Application
Les actions ayant une corrélation proche de zéro ou négative peuvent être choisies pour diversifier le portefeuille, car elles sont moins susceptibles de réagir de manière similaire aux fluctuations du marché.
Étude de Cas 2: Analyse des Données Médicales
Contexte
Un chercheur médical étudie les relations entre diverses mesures de santé, telles que l’indice de masse corporelle (IMC), la pression artérielle, et les niveaux de cholestérol pour comprendre les facteurs de risque des maladies cardiovasculaires.
Données
Les données proviennent d’examens médicaux de patients, incluant l’IMC, la pression artérielle systolique et diastolique, le cholestérol total, etc.
Code et Analyse
# Charger les données médicales
medical_data = pd.read_csv('medical_data.csv')
# Sélectionner les variables d'intérêt
health_metrics = medical_data[['BMI', 'Systolic_BP', 'Diastolic_BP', 'Cholesterol', 'Age']]
# Calculer la matrice de corrélation
correlation_matrix = health_metrics.corr()
# Visualiser la matrice de corrélation
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', linewidths=0.5)
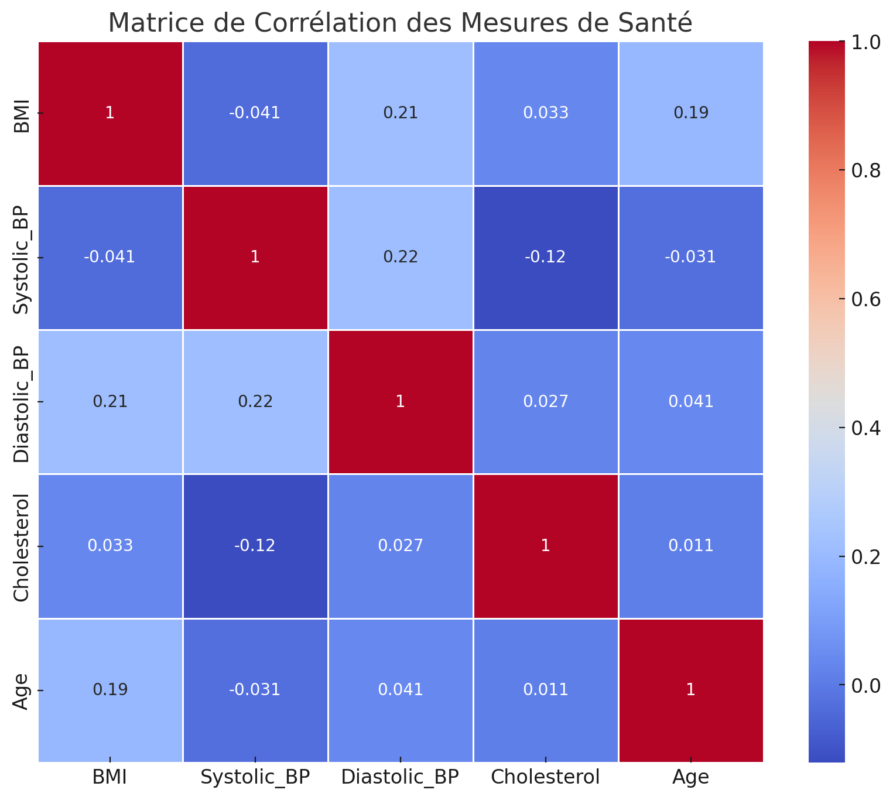
plt.title('Matrice de Corrélation des Mesures de Santé')
plt.show()Application
Identifier des corrélations élevées entre des mesures de santé spécifiques peut aider à cibler les interventions médicales. Par exemple, une forte corrélation entre l’IMC et la pression artérielle pourrait indiquer la nécessité de gérer le poids pour contrôler la pression artérielle.
Étude de Cas 3: Analyse des Données de Vente au Détail
Contexte
Un gestionnaire de magasin de détail souhaite comprendre les relations entre les ventes de différents produits pour optimiser les stratégies de merchandising et de placement des produits.
Données
Les données incluent les ventes mensuelles de différents produits dans plusieurs magasins.
Code et Analyse
# Charger les données de vente au détail
retail_data = pd.read_csv('retail_sales.csv')
# Sélectionner les variables d'intérêt
sales_data = retail_data[['Product_A', 'Product_B', 'Product_C', 'Product_D', 'Product_E']]
# Calculer la matrice de corrélation
correlation_matrix = sales_data.corr()
# Visualiser la matrice de corrélation
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', linewidths=0.5)
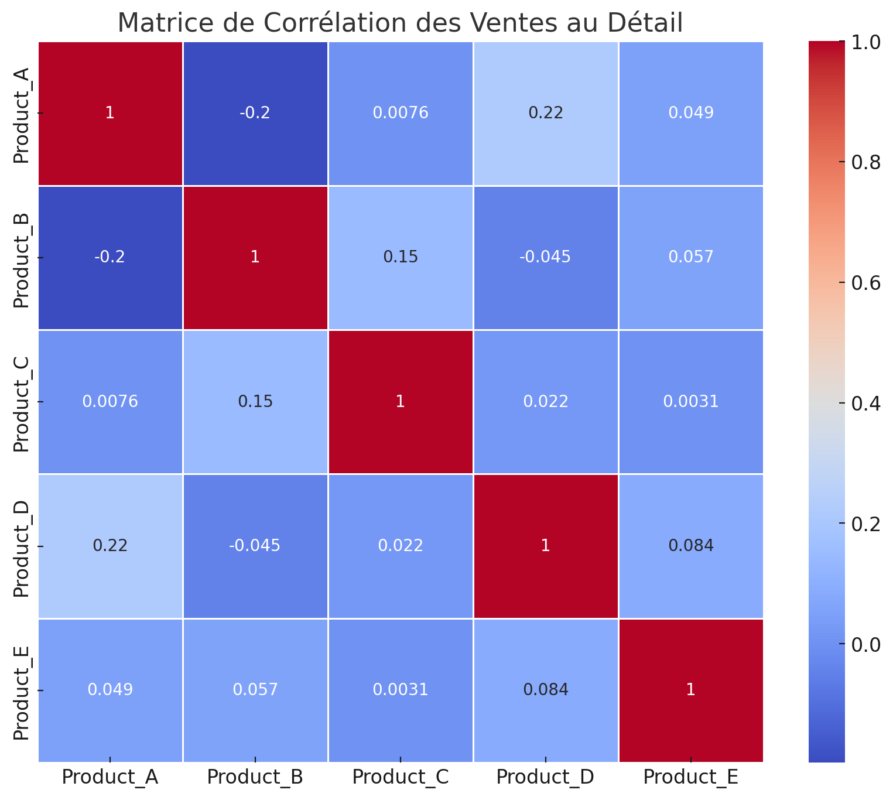
plt.title('Matrice de Corrélation des Ventes au Détail')
plt.show()Application
Comprendre quelles ventes de produits sont fortement corrélées peut aider à créer des promotions groupées et à organiser les produits de manière à maximiser les ventes croisées. Par exemple, si les ventes de Product_A et Product_B sont fortement corrélées, les placer côte à côte pourrait augmenter les ventes globales.
Applications Spécifiques de la Matrice de Corrélation avec des Cas Particuliers
Pour approfondir l’utilité de la matrice de corrélation, examinons des applications spécifiques avec des cas particuliers dans différents domaines.
Application 1: Détection de Fraude par Carte de Crédit
Contexte
Une banque souhaite identifier les transactions frauduleuses par carte de crédit en analysant les relations entre différentes caractéristiques des transactions, telles que le montant, le lieu, l’heure et la fréquence des transactions.
Données
Les données incluent des transactions par carte de crédit avec des caractéristiques telles que l’ID de la transaction, le montant, le lieu, l’heure, et une étiquette indiquant si la transaction est frauduleuse ou non.
Code et Analyse
# Charger les données de transaction
fraud_data = pd.read_csv('credit_card_transactions.csv')
# Sélectionner les variables d'intérêt
transaction_metrics = fraud_data[['amount', 'location', 'time', 'frequency', 'is_fraud']]
# Convertir les variables catégorielles en numériques
transaction_metrics['location'] = transaction_metrics['location'].astype('category').cat.codes
transaction_metrics['time'] = pd.to_datetime(transaction_metrics['time']).dt.hour
# Calculer la matrice de corrélation
correlation_matrix = transaction_metrics.corr()
# Visualiser la matrice de corrélation
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', linewidths=0.5)
plt.title('Matrice de Corrélation des Transactions par Carte de Crédit')
plt.show()Application
Identifier des corrélations entre des caractéristiques spécifiques des transactions et la variable cible (is_fraud) peut aider à détecter des modèles suspects. Par exemple, une forte corrélation entre des montants de transaction élevés et la fraude pourrait alerter la banque sur des transactions à surveiller de près.
Application 2: Analyse des Performances des Étudiants
Contexte
Une université souhaite comprendre les facteurs qui influencent les performances académiques des étudiants en analysant les relations entre les heures d’étude, la participation en classe, les notes obtenues et d’autres variables pertinentes.
Données
Les données incluent des informations sur les étudiants telles que les heures d’étude hebdomadaires, la participation en classe, les notes des examens, et les activités parascolaires.
Code et Analyse
# Charger les données des étudiants
student_data = pd.read_csv('student_performance.csv')
# Sélectionner les variables d'intérêt
performance_metrics = student_data[['study_hours', 'class_participation', 'exam_scores', 'extracurricular', 'final_grade']]
# Calculer la matrice de corrélation
correlation_matrix = performance_metrics.corr()
# Visualiser la matrice de corrélation
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', linewidths=0.5)
plt.title('Matrice de Corrélation des Performances des Étudiants')
plt.show()Application
Les corrélations entre les heures d’étude, la participation en classe et les notes finales peuvent aider à identifier les pratiques efficaces pour améliorer les performances académiques. Par exemple, si la participation en classe montre une corrélation élevée avec les notes finales, l’université pourrait encourager une participation plus active en classe.
Application 3: Optimisation des Récoltes en Agriculture
Contexte
Un agriculteur souhaite optimiser ses récoltes en analysant les relations entre diverses conditions environnementales (température, humidité, précipitations) et les rendements des cultures.
Données
Les données incluent des mesures environnementales quotidiennes et les rendements des cultures sur une période de plusieurs années.
Code et Analyse
# Charger les données agricoles
agriculture_data = pd.read_csv('crop_yields.csv')
# Sélectionner les variables d'intérêt
environmental_metrics = agriculture_data[['temperature', 'humidity', 'precipitation', 'soil_quality', 'crop_yield']]
# Calculer la matrice de corrélation
correlation_matrix = environmental_metrics.corr()
# Visualiser la matrice de corrélation
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', linewidths=0.5)
plt.title('Matrice de Corrélation des Facteurs Environnementaux et Rendements des Cultures')
plt.show()Application
Comprendre les corrélations entre les conditions environnementales et les rendements des cultures peut aider l’agriculteur à prendre des décisions éclairées sur l’irrigation, la fertilisation et la plantation. Par exemple, une forte corrélation entre l’humidité du sol et les rendements des cultures pourrait indiquer l’importance d’un bon système d’irrigation.

