Cp / Cpk : comprendre, calculer et décider — guide pratique (avec modèle “one-page”)

Les indices de capabilité Cp et Cpk quantifient à quel point un procédé tient ses limites de spécification (LSL/USL). Dans la pratique, ils transforment un nuage de mesures en un diagnostic chiffré et actionnable : le procédé est-il capable, centré, robuste ? Voici l’essentiel pour les calculer, les lire sans piège, et les relier à votre modèle Excel “one-page”.

1) Ce que mesurent Cp et Cpk

Cp mesure le potentiel de capabilité si le procédé est parfaitement centré sur la cible :

Cpk mesure la capabilité réelle, en tenant compte du décalage de la moyenne par rapport au centre de la tolérance :

Où μ\mu est la moyenne et σ\sigma l’écart-type (variabilité court terme dans l’approche classique Cp/Cpk).

À retenir :

Cp répond “le procédé est-il assez serré ?” (largeur des specs vs dispersion).
Cpk répond “le procédé est-il serré et centré ?” (dispersion et centrage).

2) Données et prérequis

Échantillons : viser ≥ 25, idéalement 50–100 mesures représentatives d’un procédé stable (pas de changements de réglages, de matière, d’équipe).
Stabilité : valider l’absence de dérive via graphique I-MR ou X̄-R si possible.
Normalité : Cp/Cpk supposent une distribution ≈ normale. En cas de non-normalité, envisager une transformation (Box-Cox/Johnson) ou des capabilités percentiles.
Mesure : fiabiliser le système de mesure (MSA / Gage R&R).
Spécifications : vérifier LSL < USL et la cible (utile pour le centrage).

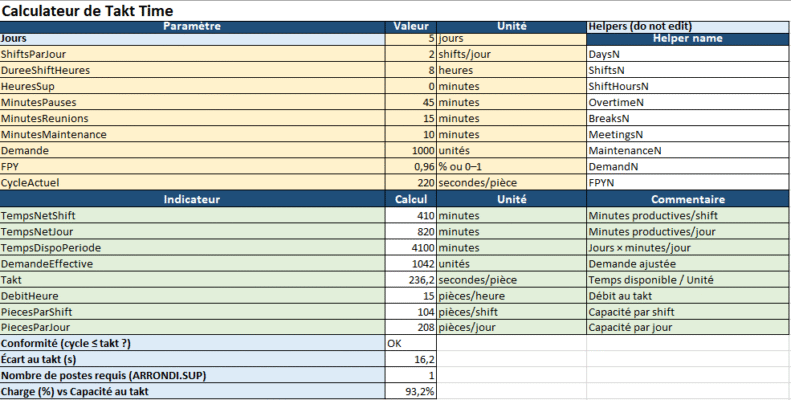
3) Mode d’emploi du modèle Excel “one-page”

Collez vos mesures en B13:B500.
Renseignez LSL, USL et Cible.
L’onglet calcule automatiquement : n, moyenne, σ = STDEV.S, Z inférieur/supérieur, % dans specs, Cp, CPU, CPL, Cpk et un statut coloré.
L’encart “OK / ⚠” vous alerte si LSL ≥ USL.
La sparkline donne une tendance visuelle rapide.

Astuce : si vous importez des données depuis un autre logiciel, collez en valeurs (sans format) pour éviter que des nombres restent en texte.

4) Exemple chiffré (lecture pas à pas)

Disons LSL = 9,90 ; USL = 10,10 ; µ = 10,02 ; σ = 0,030.

Interprétation : la dispersion pourrait passer (Cp>1), mais la moyenne est décalée vers l’USL → Cpk < 1 : non capable en l’état. La priorité n’est pas de réduire σ mais de recentrer le procédé (réglage, consigne, biais).

5) Seuils usuels et décisions

Cpk ≥ 1,33 : capable (standard industriel courant).
Cpk ≥ 1,67 : exigence sévère (sécurité/critique).
Cpk ≈ 2,00 : gamme “Six Sigma” pour un procédé centré.
Cpk < 1,00 : non capable → agir (recentrage, réduction de variabilité, revoir les specs ou le procédé).

Lisez aussi Cp :
Cp < Cpk (rare) : signe d’anomalie (vérifier les calculs).
Cp ≫ Cpk : procédé assez serré mais mal centré.
Cp ≈ Cpk : procédé bien centré ; la marge dépend surtout de σ.

6) Erreurs fréquentes… et parades

Procédé instable (dérive, lots mélangés) → Cpk “moyenné” trompeur.
Parade : segmenter par lot/poste/matière ; vérifier des cartes de contrôle.
Non-normalité marquée (asymétrie, bicarte) → extrapolations erronées.
Parade : transformation (Box-Cox) ou indices basés sur percentiles.
Système de mesure incertain (Gage R&R > 10–20 %) → σ gonflé.
Parade : fiabiliser la mesure avant d’évaluer la capabilité.
Se concentrer sur Cp seul → oublier le centrage.
Parade : toujours rapporter Cp & Cpk (et CPU/CPL).
Données trop peu nombreuses (n≈10) → indices volatils.
Parade : viser n≥25 (mieux 50–100).
LSL/USL incorrects (copiés à l’envers, mauvaise unité).
Parade : vérification croisée et conversion d’unités.

7) Et les indices Pp / Ppk (long terme) ?

Pp/Ppk évaluent la capabilité long terme (toutes sources de variabilité confondues). Les formules sont analogues en remplaçant σ\sigma “court terme” par la dispersion totale

Lecture combinée :

Cpk ≫ Ppk : procédé bien réglé en court terme, mais dérives/variations entre lots, équipes, saisons…
Cpk ≈ Ppk : comportement cohérent court/long terme.

8) Mini-checklist avant diffusion d’un Cp/Cpk

Procédé stable pendant l’échantillonnage
n ≥ 25 (idéal 50–100)
MSA/Gage R&R satisfaisant
Normalité raisonnable (ou approche alternative)
Cp, CPU, CPL, Cpk tous reportés + commentaire
Décision jointe (recentrage, réduction σ, revue specs, plan d’action)

Cp/Cpk ne sont pas qu’un “score” : ce sont des leviers de décision.

Cp vous dit si la variabilité est compatible avec la tolérance.
Cpk vous dit si, en pratique, le procédé respecte les specs compte tenu du centrage.
Avec des données fiables et un procédé stable, votre modèle “one-page” permet de calculer vite, lire clair, et agir : recentrer si Cpk est bridé par le biais, réduire la variabilité si Cp est faible, ou consolider quand les deux sont au vert.

Modèle Excel “One Page” Cp/Cpk — description

Vue d’ensemble

Un seul onglet CpCpk_OnePage prêt à imprimer (1 page). Vous collez vos mesures en colonne B, vous saisissez LSL/USL/Cible, et le classeur calcule automatiquement n, moyenne, σ, % dans specs, Cp, CPU/CPL, Cpk + un statut coloré.

Structure de la feuille

1) En-tête

B1:N1 – Titre : “Modèle simplifié – Indices de capabilité Cp / Cpk (One Page)”.

2) Paramètres (entrées)

Bloc B3:D8.
C4 = LSL, C5 = USL, C6 = Cible, C7 = Unité, C8 = Décimales.
D4 contrôle de cohérence :
=IF(C4>=C5,"⚠ LSL doit être < USL","OK")
(vert si OK, rouge sinon).

3) Statistiques (calculées)

Bloc E3:H8.
- n (F4) : =COUNT(B13:B500)
- Moyenne (F5) : =IFERROR(AVERAGE(B13:B500),"")
- Écart-type σ (F6) : =IFERROR(STDEV.S(B13:B500),"")
- Z inf (F7) : =IF(F6="","",IF(C4="","",(F5-C4)/F6))
- Z sup (F8) : =IF(F6="","",IF(C5="","",(C5-F5)/F6))
- % dans specs (H4) : =IF(F6="","",NORM.DIST(C5,F5,F6,TRUE)-NORM.DIST(C4,F5,F6,TRUE))
- Min/Max/Amplitude (H5/H6/H7) : min, max, max-min des mesures.

4) Indices de capabilité

Bloc J3:L8.
- Cp (K4) : =(C5-C4)/(6*F6)
- CPU (K5) : =(C5-F5)/(3*F6)
- CPL (K6) : =(F5-C4)/(3*F6)
- Cpk (K7) : =MIN(K5,K6)
- Statut (K8:L8) : texte+couleur auto
  - ≥ 1,33 : Capable (vert)
  - ≥ 1,00 : Marge faible (ambre)
  - < 1,00 : Non capable (rouge)

5) Zone de données

B11:N11 – Bandeau “Mesures…”.
B12 – En-tête “Mesure”.
B13:B500 – Collez vos valeurs (50 exemples déjà saisis).
M4 – Sparkline tendance sur B13:B62 ; L4 libellé “Tendance”.

6) Notes & mise en page

B64:N66 – Conseils d’usage (où coller, comment lire).
Impression : zone B1:N66, paysage, fit to 1 page (marges serrées, centrage horizontal).

Utilisation rapide

Remplir C4–C6 (LSL/USL/Cible) et coller les mesures en B13:B500.
Lire F5/F6 (moyenne, σ) puis K4–K7 (Cp, CPU/CPL, Cpk).
Se baser sur le statut (K8:L8) pour décider : recentrer (si biais), réduire σ, ou valider.

Modele_Cp_Cpk_OnePage_v2 Download

Cas : temps de démarrage (TTI) d’une app mobile

Équipe mobile : on veut garantir un Time To Interactive (TTI) < 2,20 s sur 95 % des appareils. On suit le TTI sur chaque build via télémétrie.

Spécification : USL = 2,20 s (seuil max).
Côté unique : pas de vraie limite inférieure → on met LSL = 0 s dans le fichier (cas “one-sided”).
Échantillon : 60 démarrages mesurés (collés en B13:B500).

Mesures (exemple)

Moyenne μ=1,60 s ; écart-type σ=0,15

Calculs (dans le modèle)

Que décider ?

OK pour release : Cpk ≈ 1,33 → on tient la marge.
Mettre un garde-fou CI/CD : “bloquer la release si Cpk < 1,33 ou si la moyenne > 1,80 s”.
En suivi : tracer CPU (côté critique) build-par-build.

Si Cpk chute (< 1,00)

Plan d’action prioritaire côté centrage et/ou dispersion :

Recentrer : lazy-load des modules lourds, différer analytics/init SDK, optimiser cold start.
Réduire σ : paralléliser I/O, stabiliser la chaîne (assets, réseau, device gates), réduire variance entre devices.
Segmenter : Cpk par plateforme / device-tier (bas de gamme vs haut de gamme).

Paramétrage dans votre Excel

C4 (LSL) = 0 ; C5 (USL) = 2,20 ; C7 (Unité) = s.
Collez les TTI en B13:B500 → le modèle calcule CPU/CPL/Cpk et colore le statut.
Pour une spec purement unilatérale, basez la décision surtout sur CPU (et donc Cpk = CPU ici).