Tutoriel Excel : calculer l’écart type S2 en utilisant Excel
Recommandés
Dans ce tutoriel excel, nous montrons un cas d’usage d’Excel pour les statistiques.
tutoriel excel / tutoriel excel pour la finane / tutoriel excel pour les statistiques
La variance est une formule qui indique à quel point les points que nous avons xi diffèrent de la moyenne.
Écart type :
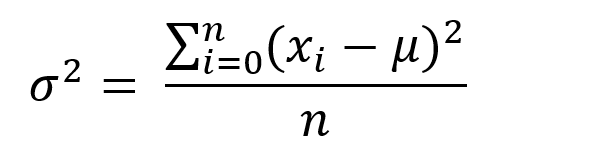
Pour le calculer dans Excel nous utilisons la formule VAR.P qui est la variance qui prend en compte toute la population selon la formule suivante :
Notation :
σ2 = écart
xi = point unique i
μ = moyenne des points
n = nombre de points
On calcule à quel point chaque point xi diffère de la moyenne, les distances (au carré) sont additionnées, puis le résultat est divisé par le nombre de points dans la population. On obtient ainsi la « distance moyenne à la valeur moyenne ». Les distances individuelles sont considérées comme quadratiques pour rendre positives les distances négatives des points individuels par rapport à la moyenne.
Exemple
Sur une feuille Excel, nous avons collecté une série de valeurs de température. Nous voulons calculer la variance de ceux-ci.
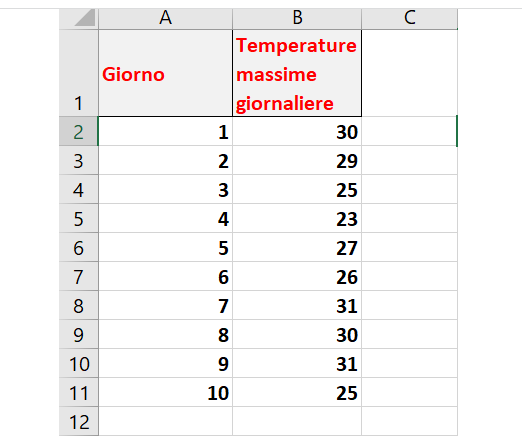
Nous cliquons sur une cellule vide et écrivons la fonction VAR.P pour implémenter la formule d’intérêt. Nous passerons toutes les valeurs de température à la formule.
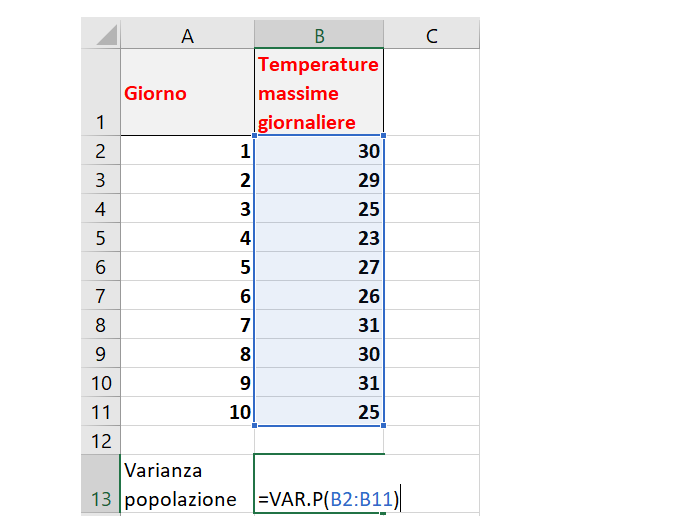
Et voici le résultat final :
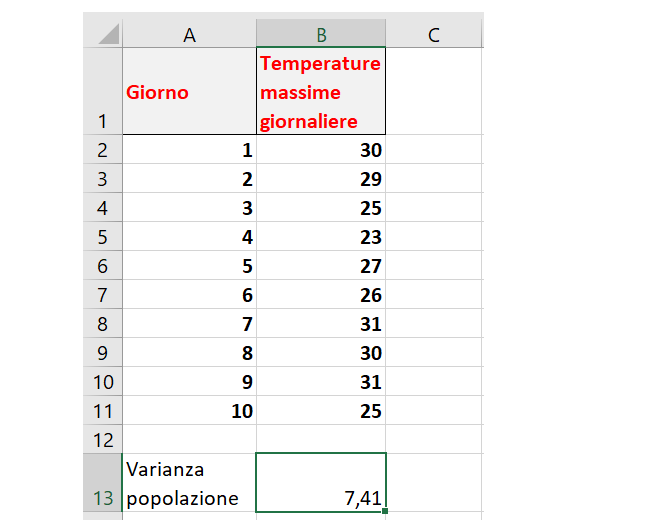
Excel pour les statistiques / La variance de l’échantillon
La variance de l’échantillon est utilisée lorsque vous avez l’intention de calculer la variance dans un sous-ensemble de l’univers de points (tous les points dans notre feuille Excel).
La formule mathématique est la suivante :
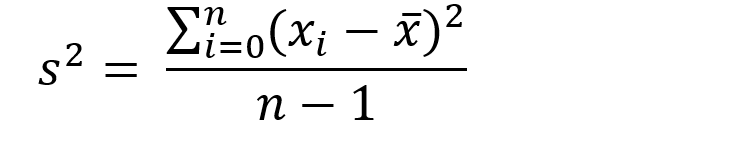
Notations
s2 = écart
xi = point unique i
x̅ = moyenne des points
n = nombre de points
La formule de calcul de la variance de l’échantillon dans Excel est VAR.C.
Exemple
En utilisant les valeurs de température précédemment collectées, nous voulons calculer la variance des cinq premiers. Comme nous n’opérons pas sur l’ensemble de la population de valeurs stockées dans notre feuille Excel, nous utilisons la formule de la variance de l’échantillon.
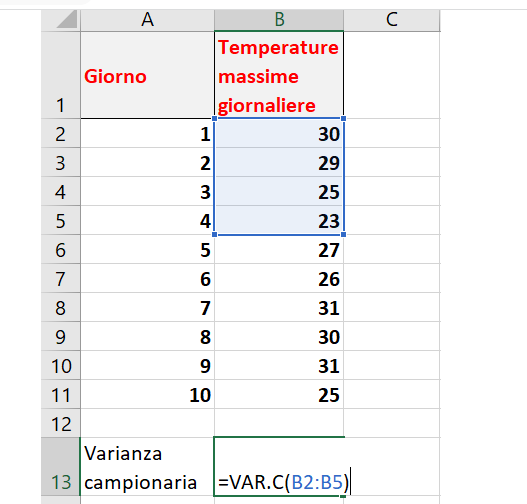
Et voici le résultat final :
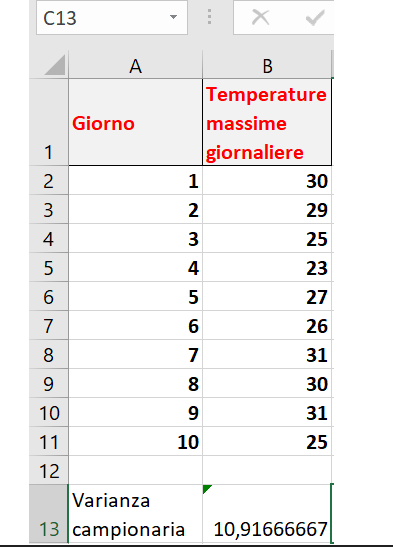
Laquelle des deux formules appliquer ?
Si nous avons 100 points et que nous voulons calculer la variance de tous les points, nous sélectionnons tous les points et utilisons la fonction VAR.P sur cet intervalle. La formule appliquée dans ce cas sera donc la formule de la variance sur l’ensemble de la population σ2.
Si, par contre, nous voulons calculer la variance d’un sous-ensemble de ceux-ci, par exemple les 50 premiers, nous utiliserons la formule de variance de l’échantillon S2.