statistique descriptive à une dimension : Exercice pratique
Recommandés
Introduction cours statistique descriptive à une dimension : Les points relevant de l’analyse statistique descriptive et qui seront décrits dans ce chapitre sont généralement liés à:
Les séries et les tableaux statistiques;
✓Les representations graphiques;
✓Les développements nécessaires au calcul statistique des différentes caractéristiques des populations étudiées et qui sont jugées nécessaires selon l’analyse et l’objectif de l’utilisateur;
✓L’analyse des principales familles de caractéristiques notamment de tendance centrale, de dispersion et de concentration,…
En effet, le premier outil nécessaire dans la réduction statistique descriptive demeure le tableau statistique qui nous donne effectivement T’avantage de constituer un premier jugement sur la population étudiée.
L’analyse peut être mieux présentée aussi via un second outil représenté par la représentation graphique de la base de données qui, elle, suggère la maîtrise de certaines règles d’établissement vu que les types se différent alors que le choix est indéniable.
Le troisième outil est représenté par les différents paramètres qui sont jugés significatifs de plusieurs aspects de la distribution statistique.
On cite à cet égard:
d’abord, les des caractéristiques de tendance centrale CTC tels que le mode, la médiane, la médiale et les moyennes ainsi que les moments qui restent essentielles mais généralement pas suffisantes dans un travail d’observation.
Ensuite, les caractéristiques de dispersion telles que la variance et l’écart type, les quartiles, les déciles,les centiles, le coefficient de variation, … qui donnent, certes, un plus relativement aux CTC mais qui peuvent être améliorés.
Enfin, les caractéristiques de concentration notamment l’indice de Gini, la courbe de Lorenz et le coefficient de concentration qui permettent de mesurer le degré de répartition des individus et des masses comme la masse salariale répartie entre les employé d’une entreprise.
Deux autres objectifs peuvent être encore rappelés mais qui développés dans les autres chapitres concernent :
La constitution des jugements sur les séries statistiques via essentiellement les résultats des caractéristiques précitées.
Et la préparation des décisions, actuelles ou futures, dans le cadre de la gestion quotidienne de l’entreprise ou la gestion prévisionnelle des projets.
Exercices n°1 – statistique descriptive
Dans une école de formation de 600 étudiants on a enregistré les notes
moyennes annuelles suivantes :
35% des étudiants ont une note de 4 au plus ; 40% des étudiants ont une note de 8 au plus ;
15% des étudiants ont une note de 12 au plus ;
10% des étudiants ont une note de 16 au plus;
TAF:
1. Présenter ces données dans un tableau avec des classes de même amplitude sachant qu’il n’y a aucun étudiant qui a une note de plus de 16.
2. Calculer la moyenne et donner sa signification.
3. Calculer la médiane et donner sa signification.
4. Calculer le mode graphiquement, algébriquement et donner sa signification.
Exercice n° 2 – SD à une dimention
Une enquête menée auprès de 21 ménages, portant sur le nombre de pièces par maison a donné les résultats suivants:
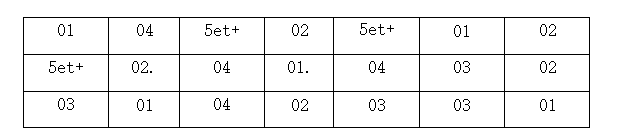
TAF:
1. Etablir la distribution de fréquence concernée.
2. Quelle est la nature de la série, de la population et du caractère utilisés.
3. Représenter graphiquement la distribution de fréquence établie.
4. Donner la distribution des fréquences cumulées et les diagrammes de fréquences cumulées.
Exercice n°3:
Dans une classe de 36 étudiants un enseignant donne distinctement les notes suivantes:
Applications de la SD à une dimension

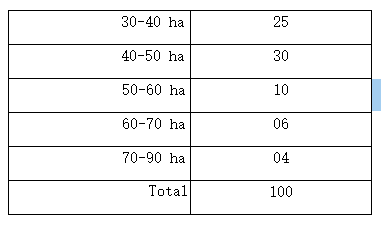
TAF
1.Représenter cette série sur le même graphe à l’aide d’un histogramme et d’un polygone de fréquences.
2. Représenter cette série sur le même graphe à l’aide d’un polygone de fréquences cumulées croissantes et d’un polygone de fréquences cumulées décroissantes.
3.Quelle est:
a) la proportion des exploitations agricoles dont la superficie est inférieure à 50 ha?
b) la proportion des exploitations agricoles dont la superficie est supérieure ou égale à 40 ha?
d) le nombre des exploitations agricoles dont la superficie est au moins de 60 ha?
e) le nombre des exploitations agricoles dont la superficie est au plus égal à 30 ha?
Exercice n°5 – Statistique descriptive à une dimenssion
Soit la population de SO salariés classes d’après le niveau de leur salaire journalier.

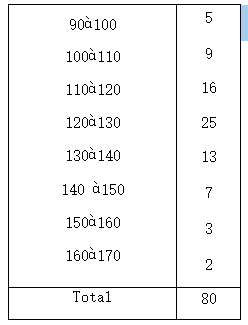
TAF:
1. Calculez les quartiles de cette distribution.
2. Trouver l’intervalle interquartile et l’intervalle absolu moyen.
3.Que peut-on déduire?
Exercice n°6:
La distribution suivante représente la répartition du diamètre des chevilles produites dans une société industrielle:

1. Calculer le diamètre moyen, médian, et modal des chevilles en question.
2. Analyser leur dispersion.
3. Que peut-on dire de leur concentration ?
Exercice n°7:
L’étude de la répartition des revenus annuels des personnes d’échantillon a donné les résultats suivants :
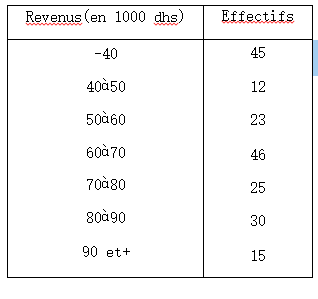
TAF:
1. Calculer les revenus annuels moyen et médian sachant qu’aucune personne ne touche moins de 1666,67 dhs par mois et que le maximum de revenu mensuel réalisé dans cette population est de 9166,67 dhs.
2. Analyser la dispersion en utilisant l’Ecart-type et le coefficient de variation.
3. Donner l’intervalle contenant 40% des revenus existant au centre de la série.
4. Recalculer la nouvelle moyenne et le nouveau CV sachant que tous les revenus annuels augmentent de 20%.
Exercice n°8:
On considère la distribution définie par le tableau ci-dessous:
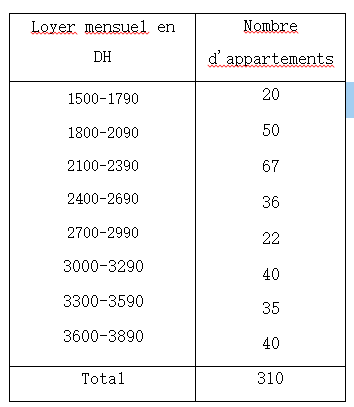
1. Peut-on représenter graphiquement cette série?
2.Représenter les valeurs modale, médiane et médiale dans celte serie.
3.Analyser la concentration des loyers mensuels par l’indice de Gimi et la courbe de Lorentz.