Fiche Méthodologique : Applications de l’Intérêt Composé
Recommandés
L’intérêt composé est un concept central en mathématiques financières. Il s’agit d’un processus où les intérêts s’accumulent non seulement sur le capital initial, mais aussi sur les intérêts déjà gagnés au fil du temps. Cet effet d’« intérêts sur les intérêts » permet de faire croître les investissements de manière plus rapide que l’intérêt simple.
Voici une fiche méthodologique sur les principales applications de l’intérêt composé, les formules associées, et des exemples d’utilisation.
1. Formule de Base de l’Intérêt Composé
Formule Générale :
Montant accumulé = Capital initial * (1 + Taux d'intérêt)^Durée
M = C * (1 + r)^t- (M) : Montant final (capital + intérêts)
- (C) : Capital initial
- (r) : Taux d’intérêt par période
- (t) : Nombre de périodes
Exemple :
Si vous investissez 1 000 € à un taux d’intérêt composé de 5 % pendant 3 ans, le montant accumulé est :
M = 1000 * (1 + 0.05)^3 = 1000 * 1.157625 = 1157.63 €2. Applications Pratiques de l’Intérêt Composé
a. Croissance des Investissements
L’application la plus courante de l’intérêt composé est dans la gestion des investissements à long terme. L’intérêt composé permet aux investisseurs de faire croître leur capital plus rapidement que l’intérêt simple.
Formule :
Montant accumulé = C * (1 + r/n)^(n*t)- (n) : Nombre de périodes de capitalisation (ex. : si les intérêts sont composés mensuellement, (n = 12)).
Exemple :
Un investisseur place 5 000 € dans un compte d’épargne à un taux de 6 % composé mensuellement pendant 5 ans.
M = 5000 * (1 + 0.06/12)^(12*5)
M = 5000 * (1 + 0.005)^60
M = 5000 * 1.34885 = 6744.25 €Après 5 ans, l’investissement vaudra 6 744,25 €.
b. Calcul de l’Inflation
L’intérêt composé est également utilisé pour ajuster les valeurs futures en fonction de l’inflation. Cela permet de prévoir l’effet de l’inflation sur le pouvoir d’achat au fil du temps.
Formule :
Valeur future = Valeur actuelle * (1 + Taux d'inflation)^tExemple :
Si l’inflation annuelle est de 2 %, combien vaudra un bien de 1 000 € dans 10 ans ?
Valeur_future = 1000 * (1 + 0.02)^10 = 1000 * 1.219 = 1 219 €Le bien coûtera 1 219 € dans 10 ans, en tenant compte de l’inflation.
c. Calcul des Emprunts (Amortissements)
Dans le cadre d’un emprunt, l’intérêt composé est utilisé pour calculer le montant à rembourser. Les mensualités sont souvent constantes, mais la répartition entre intérêts et capital varie avec le temps.
Formule des annuités :
Annuité = Capital emprunté * [r / (1 - (1 + r)^-t)]Exemple :
Un emprunt de 20 000 € à un taux d’intérêt de 5 % sur 10 ans avec des mensualités constantes.
Annuité = 20 000 * [0.05 / (1 - (1 + 0.05)^-10)] = 2 580.94 €La mensualité annuelle sera de 2 580,94 €.
d. Retraites et Pensions
L’intérêt composé est utilisé pour calculer les fonds de retraite ou de pensions nécessaires pour maintenir un niveau de vie pendant la retraite. Les cotisations mensuelles sont souvent investies et croissent à un taux composé jusqu’à la retraite.
Exemple :
Si une personne cotise 200 € par mois dans un plan de retraite pendant 20 ans à un taux composé de 4 %, le montant accumulé sera :
M = 200 * [(1 + 0.04/12)^(12*20) - 1] / (0.04/12)
M = 200 * [(1 + 0.00333)^240 - 1] / 0.00333
M = 200 * [2.20804 - 1] / 0.00333 = 73 962.18 €Après 20 ans, le fonds de retraite aura accumulé 73 962,18 €.
e. Calcul de la Durée d’un Placement avec Objectif
Lorsque l’on souhaite atteindre un objectif d’investissement, on peut utiliser l’intérêt composé pour calculer la durée nécessaire.
Formule pour la durée :
t = ln(M / C) / ln(1 + r)Exemple :
Combien de temps faut-il pour qu’un investissement de 5 000 € atteigne 10 000 € à un taux d’intérêt composé de 7 % ?
t = ln(10 000 / 5 000) / ln(1 + 0.07)
t = ln(2) / ln(1.07) = 0.6931 / 0.06766 = 10.24 ansIl faudra environ 10,24 ans pour que l’investissement double.
3. Intérêt Composé Continu
Dans certains cas, les intérêts sont composés en continu, ce qui signifie qu’ils sont recalculés et ajoutés au capital de manière infiniment fréquente.
Formule de l’intérêt composé continu :
Montant accumulé = Capital initial * e^(r*t)
M = C * e^(r*t)Exemple :
Un capital de 2 000 € placé à un taux d’intérêt composé en continu de 6 % pendant 5 ans :
M = 2000 * e^(0.06 * 5)
M = 2000 * e^(0.30) = 2000 * 1.34986 = 2 699.72 €Le montant accumulé sera de 2 699,72 € après 5 ans.
4. Facteurs Influant sur l’Intérêt Composé
Les résultats de l’intérêt composé dépendent de plusieurs facteurs :
- Taux d’intérêt : Plus le taux d’intérêt est élevé, plus le capital croît rapidement.
- Fréquence de composition : Plus les intérêts sont composés fréquemment (annuellement, semestriellement, trimestriellement, etc.), plus la croissance du capital est rapide.
- Durée : Plus l’argent reste investi longtemps, plus l’effet d’accumulation des intérêts est important (notion d’effet boule de neige).
- Montant initial et contributions régulières : Les montants initiaux et les contributions régulières (comme les cotisations de retraite) influencent grandement le montant final.
L’intérêt composé est un outil puissant qui permet de maximiser les rendements des investissements à long terme, de gérer l’impact de l’inflation, de calculer les remboursements d’emprunts, et de planifier des objectifs financiers à travers des annuités et des pensions. La maîtrise de ces concepts permet de mieux comprendre la croissance des investissements et d’optimiser les choix financiers à travers des décisions bien éclairées.
L’intérêt composé : Exercices Corrigés
Voici plusieurs exercices corrigés autour des différentes applications de l’intérêt composé, couvrant les investissements, les prêts, la planification de la retraite, les emprunts, et la croissance des entreprises.
Exercice 1 : Compte d’Épargne avec Intérêt Composé Mensuel
Énoncé
Vous déposez 3 000 € dans un compte d’épargne à un taux d’intérêt composé de 4 % par an, capitalisé mensuellement. Calculez le montant total accumulé après 5 ans.
Solution
Données :
- Capital initial : C = 3 000 €
- Taux d’intérêt annuel : ( r = 4% = 0,04 )
- Fréquence de capitalisation : ( n = 12 ) (mensuelle)
- Durée de l’investissement : ( t = 5 ) ans
Formule de l’intérêt composé mensuel :
Montant total = C * (1 + r/n)^(n * t)Calcul :
Montant total = 3 000 * (1 + 0,04/12)^(12 * 5)
Montant total = 3 000 * (1 + 0,00333)^60
Montant total = 3 000 * (1,00333)^60
Montant total = 3 000 * 1,22139
Montant total = 3 664,17 €Le montant total accumulé après 5 ans avec un intérêt composé mensuellement est de 3 664,17 €.
Exercice 2 : Planification de la Retraite avec Intérêt Composé Annuel
Énoncé
Vous décidez d’épargner 5 000 € par an pendant 20 ans dans un compte d’investissement avec un taux d’intérêt composé de 7 % par an. Quel sera le montant total accumulé à la fin de ces 20 ans ?
Solution
Données :
- Montant de l’épargne annuelle : P = 5 000 €
- Taux d’intérêt annuel : ( r = 7 % = 0,07 )
- Nombre d’années : ( t = 20 )
- Fréquence de capitalisation : ( n = 1 ) (annuelle)
Formule de l’intérêt composé pour une série de paiements annuels :
Montant total = P * [((1 + r)^n - 1) / r]Calcul :
Montant total = 5 000 * [((1 + 0,07)^20 - 1) / 0,07]
Montant total = 5 000 * [(1,07^20 - 1) / 0,07]
Montant total = 5 000 * [(3,8697 - 1) / 0,07]
Montant total = 5 000 * [2,8697 / 0,07]
Montant total = 5 000 * 40,9957
Montant total = 204 978,50 €Le montant total accumulé après 20 ans est de 204 978,50 €.
Exercice 3 : Calcul des Intérêts d’un Prêt avec Intérêt Composé Annuel
Énoncé
Vous empruntez 10 000 € à un taux d’intérêt de 5 % par an, avec capitalisation annuelle. Si vous remboursez le prêt après 4 ans, quel est le montant total à rembourser ?
Solution
Données :
- Montant emprunté : C = 10 000 €
- Taux d’intérêt annuel : ( r = 5% = 0,05 )
- Durée du prêt : ( t = 4 ) ans
- Fréquence de capitalisation : ( n = 1 ) (annuelle)
Formule de l’intérêt composé :
Montant total = C * (1 + r/n)^(n * t)Calcul :
Montant total = 10 000 * (1 + 0,05/1)^(1 * 4)
Montant total = 10 000 * (1,05)^4
Montant total = 10 000 * 1,21550625
Montant total = 12 155,06 €Le montant total à rembourser après 4 ans est de 12 155,06 €.
Exercice 4 : Comparaison de deux options de placements
Énoncé
Vous avez le choix entre deux options d’investissement :
- Option A : Investir 1 500 € à un taux d’intérêt composé de 4 % par an pendant 8 ans.
- Option B : Investir 1 500 € à un taux d’intérêt composé de 3 % par an, mais avec capitalisation trimestrielle pendant 8 ans.
Calculez le montant total de chaque option et déterminez laquelle est plus avantageuse.
Solution
Option A : Intérêt composé annuel
Données :
- Capital initial : C = 1 500 €
- Taux d’intérêt annuel : ( r = 4% = 0,04 )
- Durée : ( t = 8 ) ans
- Fréquence de capitalisation : ( n = 1 ) (annuelle)
Formule :
Montant total = C * (1 + r/n)^(n * t)Calcul :
Montant total = 1 500 * (1 + 0,04)^8
Montant total = 1 500 * (1,04)^8
Montant total = 1 500 * 1,368569
Montant total = 2 052,85 €Option B : Intérêt composé trimestriel
Données :
- Capital initial : C = 1 500 €
- Taux d’intérêt annuel : ( r = 3% = 0,03 )
- Durée : ( t = 8 ) ans
- Fréquence de capitalisation : ( n = 4 ) (trimestrielle)
Formule :
Montant total = C * (1 + r/n)^(n * t)Calcul :
Montant total = 1 500 * (1 + 0,03/4)^(4 * 8)
Montant total = 1 500 * (1 + 0,0075)^32
Montant total = 1 500 * (1,0075)^32
Montant total = 1 500 * 1,268241
Montant total = 1 902,36 €- Option A : Montant total après 8 ans = 2 052,85 €
- Option B : Montant total après 8 ans = 1 902,36 €
L’Option A est plus avantageuse, car elle génère un montant plus élevé à la fin de la période, malgré le taux d’intérêt légèrement supérieur et une capitalisation annuelle.
Exercice 5 : Croissance des Revenus d’une Entreprise avec Réinvestissement
Énoncé
Une entreprise réalise un profit annuel de 20 000 € et décide de réinvestir 50 % de ses bénéfices dans des projets de croissance, qui rapportent un rendement annuel de 6 %. Si l’entreprise maintient ce réinvestissement pendant 10 ans, quel sera le montant total de profit généré au bout des 10 ans ?
Solution
Données :
- Profit annuel réinvesti : P = 10 000 €
- Taux de rendement annuel : ( r = 6% = 0,06 )
- Durée du réinvestissement : ( t = 10 ) ans
Formule : Le montant total généré avec réinvestissement est calculé avec la formule de l’intérêt composé pour une série de paiements annuels :
Montant total = P * [((1 + r)^t - 1) / r]- Calcul :
Montant total = 10 000 * [((1 + 0,06)^10 – 1) / 0,06]
Montant total = 10 000 * [(1,06^10 – 1) / 0,06]
Montant total = 10 000 * [(1,790847 – 1) / 0,06]
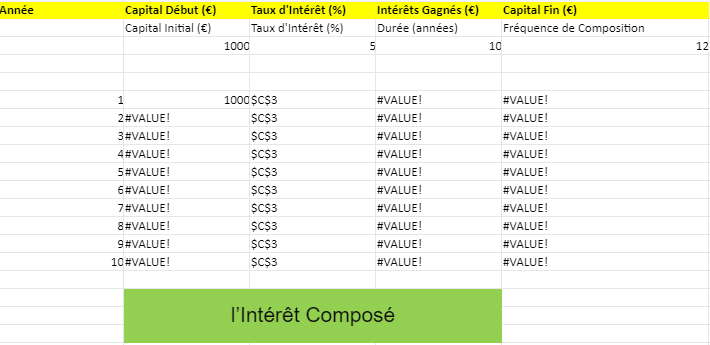
💡 Modèle Automatisé de l’Intérêt Composé
Le fichier Excel automatisé que vous venez de télécharger permet de calculer l’intérêt composé en fonction des valeurs que vous entrez. Voici un guide rapide pour l’utiliser efficacement.
Étapes d’utilisation
Ouvrir le fichier :
- Ouvrez le fichier Excel intitulé modele_automatisé_interet_compose.xlsx.
Saisie des données :
- Cellule B3 : Entrez le capital initial que vous souhaitez investir (par exemple, 5 000 €).
- Cellule C3 : Entrez le taux d’intérêt annuel en pourcentage (par exemple, 4 %).
- Cellule D3 : Indiquez la durée de l’investissement en années (par exemple, 10 ans).
- Cellule E3 : Entrez la fréquence de composition des intérêts par an (ex. : 12 pour une composition mensuelle, 4 pour trimestrielle).
Résultats automatiques :
- Le tableau de résultats commencera à partir de la ligne 6, où vous verrez le détail du calcul pour chaque année :
- Année : Numéro de l’année.
- Capital Début : Le capital au début de l’année.
- Taux d’Intérêt : Le taux d’intérêt appliqué chaque année (ce que vous avez entré en C3).
- Intérêts Gagnés : Le montant des intérêts composés gagnés pendant l’année.
- Capital Fin : Le montant total du capital après l’ajout des intérêts composés.
Visualiser les résultats :
- Les résultats pour chaque année sont automatiquement calculés et affichés dans le tableau pour une durée de 10 ans (modifiable selon vos besoins).
Exemple d’utilisation
Si vous entrez :
- Capital initial : 10 000 €
- Taux d’intérêt : 6 %
- Durée : 5 ans
- Fréquence de composition : 12 (mensuelle)
Le tableau vous montrera comment le capital évolue année après année avec les intérêts composés.
Personnalisation
Vous pouvez ajuster le modèle pour des fréquences de composition différentes (mensuelle, trimestrielle, annuelle) et des périodes plus longues en ajustant les formules dans le tableau.
Ce modèle vous aide à voir comment vos investissements croissent au fil du temps avec l’effet des intérêts composés.