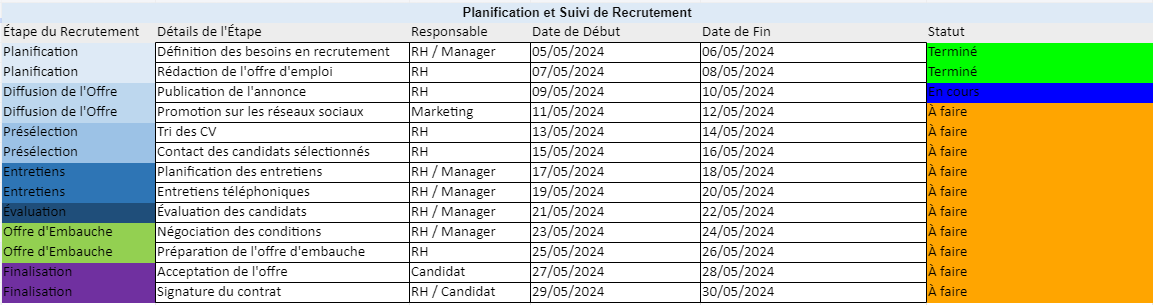
Modèle de Wilson (EOQ) — guide complet + calcul pas à pas (Excel)

Le modèle de Wilson (EOQ : Economic Order Quantity) répond à une question simple : quelle quantité commander pour minimiser le coût annuel de gestion des stocks ?
Il équilibre coût de commande et coût de possession, puis l’étend à la fiabilité d’approvisionnement (stock de sécurité, point de commande), au taux de service/fill rate, et aux contraintes d’achat (MOQ, multiple de lot).

⬇️

1) Variables & hypothèses

• D : demande annuelle (u/an)
• S : coût de passation d’une commande (€/ord)
• C : coût unitaire (€/u)
• h : taux de possession annuel (coût de stockage en % du prix, p.ex. 22 %)
• WDAYS : jours ouvrés/an
• L : délai d’approvisionnement (jours)
• σd : écart-type de la demande quotidienne (u/j)
• σL : écart-type du délai (j)
• CSL : cycle service level (probabilité de ne pas être en rupture pendant un cycle)
• MOQ, MULT : minimum de commande et multiple de lot (facultatif)

Hypothèses classiques : demande et délai stationnaires et indépendants ; coût unitaire constant (hors remises par paliers) ; réception instantanée (sans production interne continue).

2) Formules essentielles

2.1 Quantité économique de commande (EOQ)

EOQ = √( 2 × D × S / ( h × C ) )
Commandes/an = D / EOQ
Coût commandes/an = S × (D / EOQ)
Stock moyen (sans SS) = EOQ / 2
Coût possession/an = h × C × Stock_moyen
Coût logistique/an = Coût commandes + Coût possession
Coût total/an = D × C + Coût logistique

2.2 Variabilité, service, stock de sécurité et point de commande

Demande moyenne par jour : d = D / WDAYS
Variabilité sur le délai :

σLD = √( L × σd² + d² × σL² )
z = NORM.S.INV(CSL)     (ou NORMSINV en Excel « legacy »)
SS = z × σLD
ROP = d × L + SS
Couverture (jours) = ROP / d

2.3 Pénurie & fill rate (option)

Avec k = (ROP − d×L) / σLD (≈ z si SS calé sur le CSL) :

Φ(k) = NORM.S.DIST(k;VRAI)     (ou NORMSDIST)
φ(k) = NORM.DIST(k;0;1;FAUX)   (ou NORMDIST(k;0;1;FAUX))
ES (manquants/cycle) = σLD × [ φ(k) − k × (1 − Φ(k)) ]
Fill rate ≈ 1 − ES / EOQ
Coût de rupture/an = Pénalité€/u × ES × (D/EOQ)

2.4 Contraintes d’achat (MOQ/multiple)

Dans Excel :

Q_effectif = MAX(MOQ ; ARRONDI.AU.MULTIPLE(EOQ ; MULT))

Utiliser ARRONDI.SUP(EOQ/MULT;0)×MULT si ARRONDI.AU.MULTIPLE n’est pas disponible.

3) Exemple chiffré (réaliste)

Hypothèses

• D = 240 000 u/an ; S = 45 € ; C = 2,40 € ; h = 22 %
• WDAYS = 250 j ; L = 7 j → d = 960 u/j
• CSL = 95 % → z ≈ 1,645
• σd = 150 u/j ; σL = 1,5 j
• Pas de MOQ/multiple (pour commencer)

Résultats (calcul exacts)

• EOQ ≈ 6 396 u
• Commandes/an ≈ 37,5 (≈ 1 toutes 6,66 j)
• σLD ≈ 1 493,69 u ; SS ≈ 2 456,90 u
• ROP = d×L + SS ≈ 9 176,90 u (9,56 j de couverture)
• Coût commandes/an ≈ 1 688,55 €
• Stock moyen = EOQ/2 + SS ≈ 5 654,91 u
• Coût possession/an ≈ 2 985,79 €
• Coût logistique/an ≈ 4 674,34 €
• Coût total/an (incl. achats) = 240 000×2,40 + logistique ≈ 580 674,34 €
• ES/cycle ≈ 31,21 u → Fill rate ≈ 99,51 %

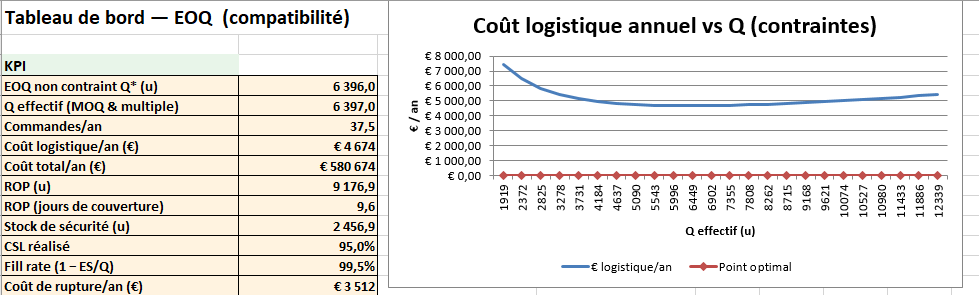
Lecture : la logistique (commandes + possession) pèse 0,8 % du coût d’achat dans cet exemple ; EOQ ≈ 6 400 u donne un fill rate ≈ 99,5 % avec CSL = 95 %.

4) Mise en œuvre dans Excel (formules FR)

• EOQ : =RACINE(2*D*S/(h*C))
• z (95 %) : =NORM.S.INV(0,95) ou =NORMSINV(0,95)
• σLD : =RACINE(L*SIGMAD^2 + (D/WDAYS)^2*SIGMAL^2)
• SS : =z*σLD
• ROP : =(D/WDAYS)*L + SS
• ES/cycle : =σLD*(NORM.DIST(k;0;1;FAUX) - k*(1-NORM.S.DIST(k;VRAI)))
  (compat : NORMDIST, NORMSDIST)
• Fill rate : =1 - ES/EOQ
• Q_effectif (MOQ/multiple) : =MAX(MOQ;ARRONDI.SUP(EOQ/MULT;0)*MULT)

Astuce compatibilité : sur d’anciennes versions/localisations, remplacez NORM.S.INV/NORM.S.DIST par NORMSINV/NORMSDIST et utilisez le séparateur ; au lieu de , si Excel le demande.

5) Quand adapter ou éviter EOQ

• Remises par paliers : passez à l’EOQ avec prix dégressifs (calculez le coût total à chaque palier et choisissez le minimum faisable).
• Saisonnalité forte / promotions : basculez en périodes (mensuel/trimestriel) et recalibrez D, h, σd, σL.
• Capacité/stock max : imposez une borne supérieure à Q.
• Périssables : considérez la durée de vie et un taux d’obsolescence dans h.
• Production interne : utilisez le modèle POQ (production lot-for-lot) au lieu d’EOQ.

6) À éviter absolument

1. Confondre h : le taux de possession est annuel et appliqué au prix (h×C).
2. Oublier le SS : EOQ minimise le coût, mais le service client dépend de ROP = d×L + SS.
3. Mélanger unités : D en u/an, d en u/j, L en jours, σd en u/j → gardez la cohérence.
4. Ignorer MOQ/multiple : arrondissez vers le haut (ARRONDI.SUP) puis MULT.
5. Fonctions Excel non reconnues : utilisez les fonctions “legacy” (NORMSINV, NORMSDIST, NORMDIST).

7) Checklist de déploiement

• Validez D, S, C, h avec Finance & Supply.
• Mesurez L, σd, σL (historique 6–12 mois).
• Fixez un CSL cible (95–98 % typique).
• Calculez EOQ, SS, ROP puis testez fill rate et coût.
• Appliquez MOQ/MULT et comparez Q_effectif vs EOQ.
• Mettez en place un rituel mensuel : revue de D, L, service, coûts.

Modèle de Wilson (EOQ) –Calculateur Excel prêt à l’emploi

Le calculateur EOQ (Wilson) vous aide à déterminer, en quelques minutes, la quantité économique de commande, le stock de sécurité et le point de commande qui minimisent vos coûts de stock. Entrez simplement vos données (demande, coût de commande, coût unitaire, taux de possession, délai…) dans les cellules bleues : le fichier calcule automatiquement les KPI, le taux de service/fill rate et affiche la courbe du coût optimal. Compatible toutes versions d’Excel, il intègre aussi les contraintes MOQ/multiples et un coût de rupture optionnel pour des décisions opérationnelles fiables.

1) But du classeur

Un calculateur EOQ (Wilson) complet et compatible toutes versions Excel, qui détermine :

• la quantité économique de commande (EOQ),
• le stock de sécurité (SS) et le point de commande (ROP),
• le taux de service (CSL), un fill rate approximatif,
• l’impact des contraintes d’achat (MOQ, multiple de lot),
• les coûts annuels (commande, possession, logistique, total) et un graphique du point optimal.

Version “compat” : j’utilise NORMSINV / NORMSDIST / NORMDIST à la place de NORM.S.* pour éviter l’erreur #NOM? selon les versions/localisations d’Excel.

2) Feuilles & organisation

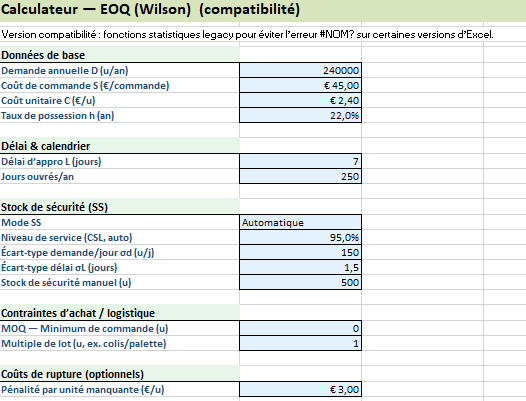
Onglet « Paramètres »

• Cellules bleues = à modifier :
  • D (demande/an), S (€/commande), C (€/u), h (taux de possession/an)
  • L (délai en jours), Jours ouvrés/an
  • Mode SS (Automatique/Manuel)
  • CSL (niveau de service cible), σd (écart-type demande/jour), σL (écart-type délai)
  • MOQ (minimum de commande), MULT (multiple de lot), PEN (pénalité €/u manquante – optionnelle)

Onglet « Calculs »

• EOQ non contraint : =RACINE(2*D*S/(h*C))
• Q effectif (MOQ & multiple) : =MAX(MOQ;ARRONDI.SUP(EOQ/MULT;0)*MULT)
• d (u/j) = D / JoursOuvrés ; σLD = √( L*σd² + d²*σL² )
• z = NORMSINV(CSL) ; SS auto = z*σLD ; SS retenu = (Auto ou Manuel)
• ROP (u) = d*L + SS ; Couverture = ROP / d
• Stock moyen (u) = Q/2 + SS
• Coûts/an :
  • Commandes = S * (D/Q)
  • Possession = h * C * Stock_moyen
  • Logistique = Commandes + Possession
  • Total = D*C + Logistique
• Service & ruptures (option) :
  • k = (ROP − d*L)/σLD ; Φ(k) = NORMSDIST(k) ; φ(k) = NORMDIST(k;0;1;FAUX)
  • ES (manquants/cycle) = σLD*(φ(k) − k*(1−Φ(k)))
  • Manquants/an = ES * (D/Q) ; Coût de rupture = PEN * Manquants/an

Onglet « Courbe »

• Tableau Q proposé → Q effectif, commandes/an, € commande/an, € possession/an, € logistique/an, fill rate.
• Mise en évidence du Q optimal (coût logistique minimal).
• Sert de source au graphique.

Onglet « Dashboard »

• KPI : EOQ non contraint, Q effectif, commandes/an, ROP (u & jours), SS, CSL réalisé, fill rate, € logistique/an, € total/an, € rupture/an.
• Graphique ligne : coût logistique annuel vs Q effectif avec marqueur du minimum.

Onglet « Mode d’emploi »

• Pas-à-pas, rappel des formules, conseils (compatibilité, saisonnalité, SS manuel, etc.).

3) Ce que vous changez / ce qui se calcule

• Vous changez uniquement les cellules bleues de « Paramètres ».
• Tout le reste (EOQ, ROP, coûts, fill rate, courbe, KPI) se met à jour automatiquement.

4) Compatibilité & séparateurs

• Si Excel vous propose des ; au lieu des , : acceptez (Excel convertit).
• Les fonctions NORMSINV/NORMSDIST/NORMDIST évitent #NOM? sur les éditions FR/anciennes.

5) Utilisation express (1 minute)

1. Ouvrez Paramètres, ajustez D, S, C, h, L, jours ouvrés.
2. Choisissez Mode SS (Auto avec CSL/σd/σL ou Manuel).
3. Si besoin, renseignez MOQ/MULT et PEN.
4. Lisez Dashboard (KPI) et le graphique pour le Q optimal.

Cas particuliers EOQ : 10 situations à connaître (formules incluses)

Ci-après une série de cas particuliers autour d’EOQ (Wilson), chacun rédigé différemment et avec les formules codifiées.
Notation utile : (H = h X C) est le coût de possession annuel par unité (€/u/an).

1) Remises par paliers (prix dégressifs)

Quand le prix unitaire baisse au-delà de certains seuils, le « meilleur » (Q) n’est pas forcément l’EOQ « théorique ». On évalue le coût total à l’EOQ de chaque palier et au point de rupture de prix, puis on retient le minimum faisable.

Pour le palier i (prix Ci, seuil Qi_min) :
EOQ_i = √( 2 D S / (h Ci) )

TC(Q ; Ci) = D·Ci + S·(D/Q) + (h·Ci)·(Q/2 + SS)

Tester : Q = max(EOQ_i, Qi_min) et Q = Qi_min
Choisir le Q (et Ci) donnant le TC minimal

2) Ruptures autorisées (retards servis/backorders)

Si l’on tolère des retards servis avec pénalité (P) (€/u/an), l’optimum change : on commande plus souvent et on accepte un reliquat à servir.

H = h·C
Q* = √( 2 D S (H + P) / (H·P) )
B* = (H / (H + P)) · Q*      (backorders max)
Stock_moyen = ( (Q* − B*) / 2 )
Coût_total_log = S·(D/Q*) + H·Stock_moyen + P·(B*/2)·(D/Q*)

3) Produits périssables (durée de vie)

Pour des articles à durée de vie (T) (jours), on borne la taille de lot : le cycle ne doit pas excéder (T), sinon on jette.

d = D / WDAYS
Contrôle de faisabilité :  Q ≤ d · T
Si Q_théorique > d·T : prendre Q = d·T (ou plus petit multiple logistique)

4) Production interne (POQ au lieu de réception instantanée)

Quand on produit à débit (P) (u/an) avec (P > D), le stock se remplit progressivement. L’optimum (POQ) tient compte du taux de consommation pendant la fabrication.

H = h·C
Q*POQ = √( (2 D S / H) · ( P / (P − D) ) )
Stock_moyen = (Q*POQ / 2) · (1 − D/P)
Coût_log = S·(D/Q*POQ) + H·Stock_moyen

5) Capacité de stockage (contrainte “K”)

Un stock max (hors SS) limite le lot. On « clippe » l’EOQ et on respecte les multiples d’emballage.

Capacité utile = K − SS
Borne sur Q :   Q ≤ 2 · (K − SS)

Q_feasible = min( EOQ , 2·(K − SS) )
Q_effectif = max( MOQ , ceil(Q_feasible / MULT) · MULT )

6) Demande non stationnaire (saisonnalité) — lot sizing dynamique

Avec une demande par périodes (d_t) variable, l’EOQ constant n’est plus optimal. On bascule sur du Wagner-Whitin (programmation dynamique) pour minimiser coûts de commande + possession.

H = h·C (par période)
F(t) = coût minimal pour couvrir d1..dt
F(t) = min_{1≤k≤t} [ F(k−1) + S + H · Σ_{j=k}^{t} (j−k) · d_j ]
Politique : commander en k pour couvrir k..t* qui minimise F(t)

7) Service par fill rate cible (β-service)

Si la cible porte sur le taux de service en quantité (β), on dimensionne le SS via la fonction de perte (L(z)).

σLD = √( L·σd² + d²·σL² )
L(z) = φ(z) − z · (1 − Φ(z))
Objectif :  ES = L(z) · σLD  ≈  (1 − β) · Q

Résoudre z :  L(z) = (1 − β) · Q / σLD
Puis SS = z · σLD

8) Corrélation demande–délai (σLD corrigé)

Si la demande journalière et le délai sont corrélés (ex. délais ↑ quand la demande ↑), la variance sur le délai augmente.

Approximation :
σLD² ≈ L·σd² + d²·σL² + 2·d·Cov(d, L)

(où d = moyenne journalière, L = moyenne du délai)
SS = z · σLD  avec ce σLD corrigé

9) Frais de transport « par paliers » (S effectif dépend de Q)

Quand le fret varie par tranches (colis, palette, camion), le coût de commande n’est plus constant. On travaille par grille de Q faisables (multiples) et on évalue (S(Q)).

S_effectif(Q) = S_admin + Freight(Q)
TC(Q) = D·C + S_effectif(Q)·(D/Q) + H·(Q/2 + SS)

Algorithme : balayer Q ∈ { MOQ, MOQ+MULT, … } et choisir le TC minimal

10) Multi-échelon & centralisation (effet « √n »)

En consolidant (n) entrepôts indépendants en un central, la variabilité s’agrège au √n (et pas en (n)), d’où un gain de SS.

SS_décentralisé ≈ n · z · σ · √L
SS_centralisé  ≈ z · σ · √L · √n
Économie relative ≈ 1 − 1/√n

Rappel pratique (pour Excel)

• Toujours poser (H = h·C) avant d’appliquer les variantes.
• Quand une contrainte (MOQ, MULT, K, prix par paliers) existe, on calcule d’abord l’optimum théorique (EOQ/POQ), puis on projette sur l’ensemble des (Q) faisables et on choisit le coût total minimal (commande + possession ± rupture).
• Pour les fonctions stats : NORMSINV/NORMSDIST/NORMDIST assurent la compatibilité si NORM.S.* n’est pas reconnu.