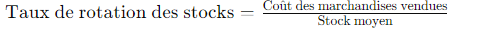Tutoriel complet : Outils de gestion de production : Pareto, Petri…
Recommandés
La gestion de production revêt une première importance pour toute entreprise cherchant à maximiser l’efficience opérationnelle et à optimiser ses ressources. Parmi les nombreux outils disponibles, deux concepts importants sont le diagramme de Pareto et les réseaux de Petri. Dans ce tutoriel, nous allons explorer ces outils en détail et discuter de leur utilisation dans la gestion de la production.
1. Diagramme de Pareto
Le diagramme de Pareto, également connu sous le nom de loi des 80/20, est un outil de gestion de la qualité qui aide à identifier et à prioriser les problèmes ou les causes de problèmes dans un processus donné. Voici comment le créer et l’utiliser :
Étapes pour créer un diagramme de Pareto :
- Collecte des données : Identifiez le problème ou le processus que vous souhaitez analyser et collectez les données pertinentes.
- Catégorisation : Classez les données en différentes catégories ou causes possibles du problème.
- Calcul des fréquences : Comptez combien de fois chaque catégorie apparaît dans les données.
- Calcul du pourcentage cumulé : Calculez le pourcentage cumulé de chaque catégorie par rapport au total.
- Tracé du diagramme : Tracez un diagramme à barres où les catégories sont représentées sur l’axe horizontal et les fréquences (ou pourcentages cumulés) sur l’axe vertical.
- Analyse : Identifiez les catégories qui contribuent le plus aux problèmes en se concentrant sur les catégories ayant les fréquences les plus élevées ou les pourcentages cumulés les plus importants.
Exemple d’utilisation :
Supposons que vous êtes responsable de la qualité dans une usine de fabrication de voitures. Vous voulez identifier les défauts les plus fréquents dans la production. Après avoir collecté les données sur les défauts rencontrés, vous pouvez créer un diagramme de Pareto pour visualiser les principales causes de défauts et prioriser les actions correctives en conséquence.
2. Réseaux de Petri
Les réseaux de Petri sont des outils de modélisation et d’analyse des systèmes dynamiques, particulièrement utiles pour représenter les processus concurrents ou simultanés. Voici comment les utiliser :
Éléments des réseaux de Petri :
- Places : Représentent les états ou les conditions du système.
- Transitions : Représentent les événements ou les actions qui changent l’état du système.
- Arcs : Relient les places aux transitions (et vice versa) et représentent les conditions préalables à l’activation d’une transition.
Exemple d’utilisation :
Imaginons que vous souhaitez modéliser le processus de fabrication d’un produit dans une usine. Vous pouvez représenter chaque étape du processus comme une place et chaque action (comme l’assemblage d’une pièce) comme une transition. Les arcs indiquent les conditions préalables à l’exécution de chaque action.
3. Utilisation avancée du Diagramme de Pareto
Analyse des Causes Racines :
Une utilisation avancée du diagramme de Pareto consiste à aller au-delà de l’identification des problèmes les plus fréquents pour comprendre les causes sous-jacentes. Pour chaque catégorie identifiée dans le diagramme de Pareto, vous pouvez creuser plus en profondeur en utilisant des outils comme le diagramme d’Ishikawa (aussi appelé diagramme en arêtes de poisson) pour identifier les causes racines. Cela permet une approche plus ciblée dans le processus de résolution des problèmes, en s’attaquant directement aux sources principales des problèmes plutôt qu’aux symptômes.
Suivi des Améliorations :
Une fois vous mettez en place des actions correctives pour résoudre les problèmes identifiés, il est crucial de suivre l’efficacité de ces actions. Le diagramme de Pareto peut être utilisé à nouveau pour comparer les données avant et après l’implémentation des solutions. Cela permet de visualiser si les améliorations ont eu l’impact attendu et de déterminer si d’autres ajustements sont nécessaires.
4. Applications avancées des Réseaux de Petri
Modélisation de Systèmes Complexes :
Les réseaux de Petri peuvent être utilisés pour modéliser des systèmes complexes où plusieurs processus se déroulent simultanément et interagissent les uns avec les autres. Par exemple, dans le domaine des systèmes informatiques, les réseaux de Petri peuvent être utilisés pour modéliser le comportement des logiciels multi-tâches, où plusieurs programmes s’exécutent en parallèle et partagent des ressources telles que le processeur et la mémoire.
Analyse de Performance :
En utilisant des techniques avancées telles que la simulation, les réseaux de Petri peuvent être utilisés pour analyser la performance des systèmes et optimiser leur fonctionnement. En simulant le comportement du système sous différentes conditions et en mesurant des métriques telles que le temps d’exécution et le taux d’utilisation des ressources, les concepteurs peuvent identifier les goulots d’étranglement potentiels et proposer des améliorations pour accroître l’efficacité et la fiabilité du système.
Pour modéliser ce système de Réseaux de Petri dans Excel, vous pouvez suivre ces étapes et structurer votre modèle en trois parties principales : Places, Transitions, et Arcs. Voici une suggestion de mise en page et les étapes à suivre pour créer votre modèle dans Excel :
1. Création des tables
- Places : Créez une table avec les colonnes « ID Place », « Description », et « Marquage Initial ». Le « Marquage Initial » peut être utilisé pour indiquer si une place est active au début de la simulation (par exemple, 1 pour actif et 0 pour inactif).
- Transitions : Créez une table avec les colonnes « ID Transition » et « Description ».
- Arcs : Créez une table avec les colonnes « ID Arc », « De », « À », et « Type » (entrant/sortant).
2. Remplissage des données
- Remplissez chaque table avec les informations fournies sur les places, transitions, et arcs.
3. Visualisation
- Pour visualiser le Réseau de Petri, vous pouvez utiliser les formes d’Excel (dans l’onglet « Insertion » > « Formes ») pour représenter graphiquement les places (cercles), les transitions (rectangles), et les arcs (flèches).
Exemple de mise en page dans Excel
Places
| ID Place | Description | Marquage Initial |
|---|---|---|
| P1 | Feu rouge allumé | 1 |
| P2 | Feu vert allumé | 0 |
| P3 | Feu orange allumé | 0 |
| P4 | Voiture détectée à l’intersection | 0 |
| P5 | Aucune voiture détectée à l’intersection | 1 |
Transitions
| ID Transition | Description |
|---|---|
| T1 | Passage de feu rouge à feu vert |
| T2 | Passage de feu vert à feu orange |
| T3 | Passage de feu orange à feu rouge |
| T4 | Détection d’une voiture à l’intersection |
| T5 | Absence de voiture à l’intersection |
Arcs
| ID Arc | De | À | Type |
|---|---|---|---|
| A1 | P1 | T1 | Entrant |
| A2 | T1 | P2 | Sortant |
| … | … | … | … |
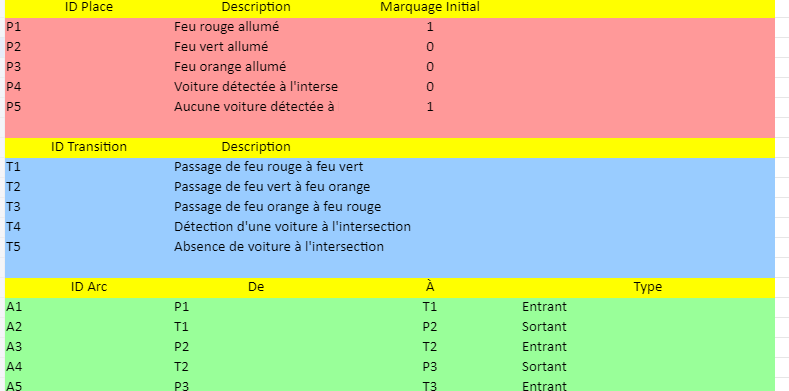
L’image ci-dessus montre une représentation visuelle du modèle de Réseaux de Petri pour un système de contrôle de feux de circulation, organisée comme elle pourrait l’être dans un tableur Excel. Cette illustration inclut les sections distinctes pour les Places, Transitions, et Arcs, ainsi que la visualisation graphique des éléments du Réseau de Petri avec des cercles pour les places, des rectangles pour les transitions, et des flèches indiquant les flux entre eux.
Conclusion
Les outils de gestion de production tels que le diagramme de Pareto et les réseaux de Petri sont essentiels pour analyser et améliorer les processus opérationnels. En utilisant ces outils de manière appropriée, les entreprises peuvent identifier les problèmes, prioriser les actions correctives et optimiser leur efficacité globale. N’oubliez pas que la clé réside dans une collecte de données précise et une analyse approfondie pour des résultats significatifs.