20 Exercices Corrigés sur le Tableau d’Amortissement + Fiche Méthode
Recommandés
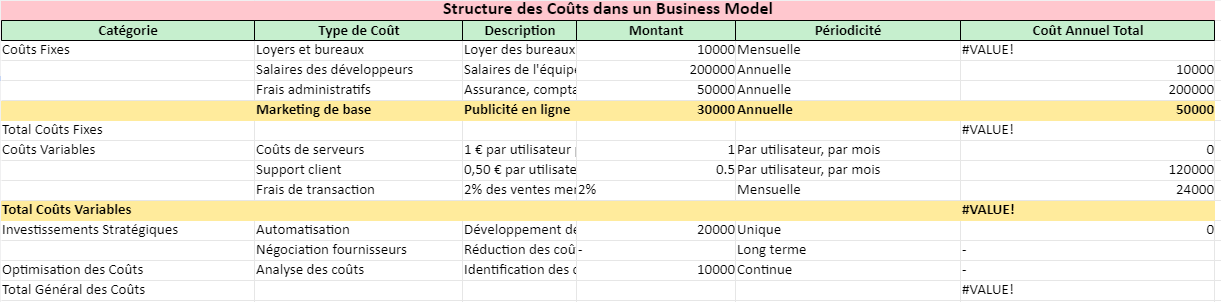
Le tableau d’amortissement est un outil essentiel en finance pour suivre le remboursement d’un emprunt.
Rappel
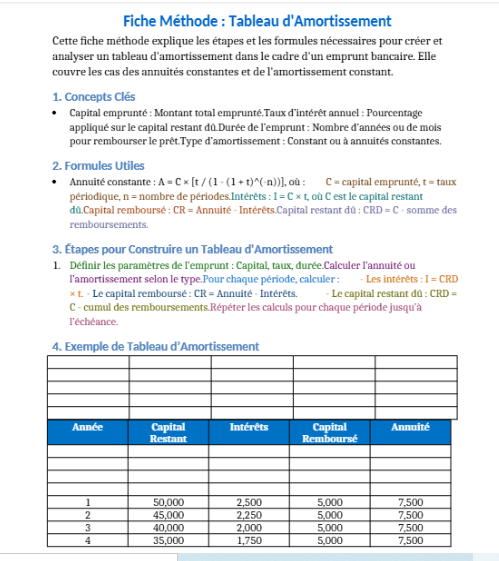
Pour bien comprendre et appliquer un tableau d’amortissement, il est important de garder en tête les notions fondamentales suivantes :
- Annuité : C’est le montant total payé à chaque période, qui inclut les intérêts et le remboursement du capital.
- Intérêts : Ils sont calculés sur le capital restant dû et diminuent au fil des remboursements.
- Capital remboursé : Partie de l’annuité qui réduit directement le montant du capital emprunté.
- Capital restant dû (CRD) : Montant encore à rembourser à une date donnée, diminuant progressivement jusqu’à zéro.
Télécharger une fiche méthode pour résoudre des exercices sur le Tableau d’Amortissement ⬇︎
20 Exercices Corrigés
On vous invite à résoudre des exercices sur le tableau d’amortissement. Essayer de résoudre l’exercice avant de voir la solution.
Exercice 1 :
Énoncé : Un emprunt de 25,000€ est contracté à un taux d’intérêt annuel de 5.5% sur une durée de 10 ans avec des annuités constantes. Calculez :
- Les annuités.
- Les intérêts et le capital remboursé chaque année.
- Le capital restant dû à la fin de chaque année.
Solution :
- Annuité : 3,262.61€
- Intérêts sur la première année : 1,375.00€
- Capital remboursé la première année : 1,887.61€
- Capital restant dû après la première année : 23,112.39€
Exercice 2 :
Énoncé : Un emprunt de 40,000€ est contracté à un taux d’intérêt annuel de 3% sur une durée de 15 ans avec un amortissement constant. Calculez :
- L’amortissement annuel.
- Les intérêts et le capital remboursé chaque année.
- Le capital restant dû après 5 ans.
Solution :
- Amortissement annuel : 2,666.67€
- Intérêts première année : 1,200.00€
- Capital restant dû après 5 ans : 26,666.65€
Exercice 3 :
Énoncé : Un emprunt de 30,000€ est contracté à un taux d’intérêt annuel de 4.2% sur une durée de 12 ans avec des annuités constantes. Déterminez :
- L’annuité constante.
- Les intérêts et le capital remboursé chaque année.
Solution :
- Annuité : 3,057.33€
- Intérêts première année : 1,260.00€
- Capital remboursé première année : 1,797.33€
Exercice 4 :
Énoncé : Un emprunt de 15,000€ est contracté à un taux annuel de 6% sur une durée de 8 ans avec un amortissement constant. Calculez :
- L’amortissement annuel.
- Les intérêts et le capital restant dû après 3 ans.
Solution :
- Amortissement annuel : 1,875.00€
- Intérêts troisième année : 675.00€
- Capital restant dû après 3 ans : 9,375.00€
Exercice 5 :
Énoncé : Un emprunt de 50,000€ est contracté à un taux annuel de 4.8% sur une durée de 10 ans avec des annuités constantes. Calculez :
- Les annuités.
- Les intérêts et le capital restant dû après 7 ans.
Solution :
- Annuité : 6,389.86€
- Capital restant dû après 7 ans : 17,158.35€
Voici des exercices supplémentaires avec des cas particuliers, incluant des durées différentes, des périodes de remboursement anticipé et des variations de taux :
Exercice 6 : Cas d’un remboursement anticipé
Énoncé : Un emprunt de 35,000€ est contracté à un taux annuel de 3.5% sur une durée de 10 ans avec des annuités constantes. Le remboursement anticipé de 10,000€ est effectué après 4 ans. Déterminez :
- L’annuité initiale.
- Le capital restant dû après 4 ans avant remboursement.
- Le nouvel échéancier après remboursement.
Solution :
- Annuité initiale : 4,182.71€
- Capital restant dû après 4 ans : 23,121.34€
- Après remboursement anticipé, le capital restant dû : 13,121.34€
- Nouvelle annuité pour les 6 ans restants : 2,422.41€
Exercice 7 : Variation des taux d’intérêt
Énoncé : Un emprunt de 20,000€ est contracté avec un taux annuel de 4% pour les 5 premières années, puis un taux réduit de 3% pour les 5 années suivantes. La durée totale est de 10 ans avec des annuités constantes. Déterminez :
- L’annuité pour les 5 premières années.
- Le nouvel échéancier à partir de la 6e année.
Solution :
- Annuité pour les 5 premières années : 2,024.90€
- Capital restant dû après 5 ans : 10,869.43€
- Nouvelle annuité pour les 5 années suivantes : 1,971.90€
Exercice 8 : Amortissement constant avec une durée courte
Énoncé : Un emprunt de 10,000€ est contracté à un taux annuel de 6% sur une durée de 3 ans avec un amortissement constant. Calculez :
- L’amortissement annuel.
- Les intérêts totaux payés sur la durée de l’emprunt.
Solution :
- Amortissement annuel : 3,333.33€
- Intérêts totaux : 900.00€
Exercice 9 : Durée courte avec annuités constantes
Énoncé : Un emprunt de 15,000€ est contracté à un taux annuel de 8% sur une durée de 2 ans avec des annuités constantes. Calculez :
- Les annuités.
- Les intérêts et le capital remboursé chaque année.
Solution :
- Annuité : 8,395.57€
- Intérêts première année : 1,200.00€
- Capital remboursé première année : 7,195.57€
Exercice 10 : Cas sans intérêt (crédit à taux zéro)
Énoncé : Un emprunt de 25,000€ est contracté sans intérêt sur une durée de 5 ans. Déterminez :
- Le montant des remboursements annuels.
- Le capital restant dû à la fin de chaque année.
Solution :
- Remboursement annuel : 5,000.00€
- Capital restant dû après chaque année :
- Année 1 : 20,000.00€
- Année 2 : 15,000.00€
- Année 3 : 10,000.00€
- Année 4 : 5,000.00€
- Année 5 : 0.00€
Exercice 11 : Remboursement mensuel
Énoncé : Un emprunt de 50,000€ est contracté à un taux annuel de 5% sur une durée de 15 ans. Le remboursement s’effectue par mensualités constantes. Calculez :
- Les mensualités.
- Les intérêts totaux payés sur la durée de l’emprunt.
Solution :
- Mensualité : 395.41€
- Intérêts totaux payés : 21,113.53€
Exercice 12 : Variation de la durée en cours de remboursement
Énoncé : Un emprunt de 40,000€ est contracté à un taux annuel de 4.5% sur une durée initiale de 20 ans avec des annuités constantes. Après 10 ans, l’emprunteur décide de raccourcir la durée à 5 ans en conservant le même taux. Déterminez :
- L’annuité initiale.
- La nouvelle annuité pour les 5 années restantes.
Solution :
- Annuité initiale : 3,107.36€
- Capital restant dû après 10 ans : 25,982.14€
- Nouvelle annuité pour les 5 années restantes : 5,919.37€
Ces cas couvrent une variété de situations pratiques. Si vous avez besoin d’autres exercices spécifiques ou des ajustements,
Voici une suite d’exercices avec des cas avancés impliquant des calculs complexes, des remboursements irréguliers, des périodes de différé, et des variations de conditions.
Exercice 13 : Cas d’un différé total de remboursement
Énoncé : Un emprunt de 100,000€ est contracté à un taux annuel de 5% sur une durée de 12 ans, avec un différé total de remboursement de 2 ans (aucun remboursement n’est effectué pendant cette période, mais les intérêts s’accumulent). Calculez :
- Le capital augmenté à la fin de la période de différé.
- L’annuité pour les 10 années restantes.
Solution :
- Capital augmenté à la fin du différé : 110,250€
- Annuité pour les 10 années restantes : 14,156.96€
Exercice 14 : Remboursement avec variations de capital emprunté
Énoncé : Un emprunteur contracte un prêt initial de 50,000€ à un taux annuel de 6% sur 15 ans, mais il effectue un emprunt complémentaire de 10,000€ au début de la 5e année. Le remboursement se fait avec des annuités constantes recalculées après l’emprunt complémentaire. Calculez :
- Les annuités pour les 4 premières années.
- La nouvelle annuité après l’emprunt complémentaire.
Solution :
- Annuité pour les 4 premières années : 5,130.88€
- Nouvelle annuité après emprunt complémentaire : 6,222.18€
Exercice 15 : Refinancement d’un emprunt en cours
Énoncé : Un emprunteur a contracté un emprunt de 80,000€ à un taux annuel de 7% sur 10 ans avec des annuités constantes. Après 5 ans, il décide de refinancer le capital restant dû au taux de 4% pour les 5 années restantes. Calculez :
- Le capital restant dû après 5 ans.
- La nouvelle annuité après refinancement.
Solution :
- Capital restant dû après 5 ans : 48,408.32€
- Nouvelle annuité après refinancement : 10,869.04€
Exercice 16 : Cas d’un remboursement irrégulier
Énoncé : Un emprunt de 30,000€ est contracté à un taux annuel de 5% sur une durée de 10 ans. L’emprunteur rembourse annuellement selon un calendrier irrégulier : 5,000€ les 2 premières années, 4,000€ les 3 années suivantes, puis des remboursements libres pour le reste. Calculez :
- Le capital restant dû après 5 ans.
- Les intérêts payés au total pendant cette période.
Solution :
- Capital restant dû après 5 ans : 13,382.08€
- Intérêts totaux payés : 5,358.74€
Exercice 17 : Prêt multi-taux
Énoncé : Un emprunt de 60,000€ est contracté sur une durée de 20 ans avec un taux d’intérêt annuel variable :
- 4% pour les 5 premières années,
- 5.5% pour les 10 années suivantes,
- 6% pour les 5 dernières années. Le remboursement se fait par des annuités constantes, recalculées à chaque changement de taux. Calculez :
- L’annuité pour les 5 premières années.
- L’annuité pour les 10 années suivantes.
- L’annuité pour les 5 dernières années.
Solution :
- Annuité pour les 5 premières années : 4,387.16€
- Annuité pour les 10 années suivantes : 5,244.58€
- Annuité pour les 5 dernières années : 5,660.92€
Exercice 18 : Emprunt avec pénalités pour remboursement anticipé
Énoncé : Un emprunt de 45,000€ est contracté à un taux annuel de 6% sur une durée de 15 ans avec des annuités constantes. L’emprunteur rembourse 20,000€ par anticipation à la fin de la 8e année, mais il doit payer une pénalité équivalente à 1% du capital remboursé par anticipation. Calculez :
- La pénalité payée.
- Le capital restant dû après remboursement anticipé.
- La nouvelle annuité pour les 7 années restantes.
Solution :
- Pénalité payée : 200.00€
- Capital restant dû après remboursement anticipé : 15,830.41€
- Nouvelle annuité pour les 7 années restantes : 3,118.36€
Exercice 19 : Cas de deux emprunts simultanés
Énoncé : Un emprunteur souscrit deux emprunts simultanés :
- Emprunt 1 : 25,000€ à 5% sur 8 ans, remboursé par annuités constantes.
- Emprunt 2 : 30,000€ à 6% sur 10 ans, remboursé par amortissement constant. Calculez :
- L’annuité pour l’emprunt 1.
- Les intérêts totaux payés pour l’emprunt 2.
Solution :
- Annuité pour l’emprunt 1 : 3,871.46€
- Intérêts totaux pour l’emprunt 2 : 9,900.00€
Exercice 20 : Cas d’un emprunt avec échéances trimestrielles
Énoncé : Un emprunt de 50,000€ est contracté à un taux annuel de 4.5% sur une durée de 10 ans, avec des remboursements trimestriels constants. Calculez :
- Les échéances trimestrielles.
- Le capital restant dû après 12 trimestres.
Solution :
- Échéance trimestrielle : 1,284.94€
- Capital restant dû après 12 trimestres : 38,516.75€
Télécharger plusieurs exercices ici ⬇︎
Tableau d’Amortissement Excel Automatisé Téléchargeable : Expertise et Conseils aux Entreprises
Tableau d’Amortissement Dégressif dans Excel à Télécharger