Tutoriel Statistique descriptive: QUELQUES EXAMENS PROPOSES
Recommandés
Bienvenue dans le tutoriel statistique descriptive
Examens de l’année 2010-11 / Examen 2ème »Session Semestre 1- 2010/1/(1h30mn)
La population d’un pays selon l’âge et le sexe pour l’année 2010
présenté comme suit:

(Il est conseillé de transformer ces données en fréquence relatives)
TAF:
1. Préciser l’unité statistique, le caractère étudié, sa nature et le nombre des modalités.
2.Quelle observation peut-on tirer du tableau?
3. Calculer selon la catégorie, l’âge moyen et le mode.
4.Montrer que l’âge moyen national est la moyenne des ages des hommes et des femmes.
5. Selon les catégories calculer le degré de dispersion de l’áge. Quelle conclusion peut-on en tirer?
6. Calculer la valeur de l’étendu qui englobe 50% des observations centrales.
7. Calculer la valeur de l’étendu qui englobe 80% des observations centrales.
Exercice n°2:
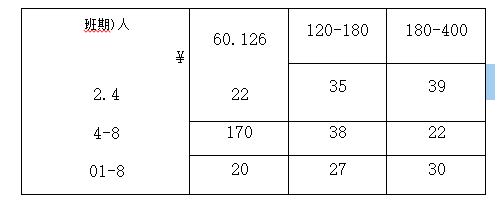
Les cadres d’une entreprise ont organisé un ‘footing” afin de tester leur forme respective. On a ainsi relevé les distances parcourues et l’âge de chacun des cadres. Le tableau suivant indique la répartition des cadres selon la distance parcourue (en Km) et l’âge (en années)

En désignant par X la distance et par Y l’âge :
1. Donner la distance moyenne marginale de X et sa signification.
2. Calculer la moyenne marginale de Y. Que nous indique-t-elle?
3. Calculer et donner la signification de:X2,3
On a calculé l’âge moyen pour chaque distance parcourue :

4. Comment a-t-on obtenu ce tableau?
5.Les deux variables Y (L’âge) et X (la distance parcourue) sont-t-elles dépendantes ou indépendantes? Justifiez votre réponse.
Exercice n°l:
Représenté l’âge de la population observée.
quantitative continue puisqu’elle est représenté par
C’est donc une variable qualitative.
La population est donnée par les 27984393 habitants de ce pays observés.
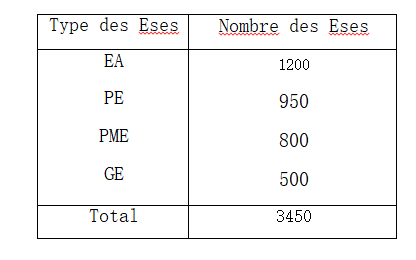
Le tableau statistique est présenté comme suit:

Puisqu’il n’y a pas d’indication sur l’âge maximum dans cette population on doit donc recourir à l’amplitude la plus fréquente qui se répété le plus grand nombre de fois. Dans cette distribution il s’agira d’une amplitude de a1=10 qui se répété trois fois alors que a2=15 figure deux fois seulement.
Le résultat fait que la borne maximale de la dernière classe soit égale à 70.
1.On présente les termes comme suit:
– L’unité statistique est représentée par « un habitant du pays concerné»
– On dispose de deux caractères:
* un quantitatif continu défnit par « l’âge de la population»
*un qualitatif nominal représenté par « la sexe de la population»
– Le nombre de modalités est de 6 modalités pour la variable X et de 2 Modalités pour la variable Y.
Ce qu’on peut constater à partir du tableau est que le nombre
des habitants diminue quand l’âge augmente et ce quelque soit le sexe
masculin ou féminin.
il faut distinguer séparément les deux d’ailleurs indiqué sur l’épreuve, par transformer les données fréquences relatives pour faciliter le calcul.
D’où les deux distributions conditionnelles de X:
Sachant les hommes:

On aura donc l’âge moyen et l’âge modal donnés par :
x=M
=Σfixxc=25,81
i=1
est d’environ 26 ans.
Ce qui signifie que lorsqu’il s’agit des
hommes, l’âge moyen dans cette population
Mo= =0+/15 (0,23-0)
(0,23-0)+(0,23-0,21)
=13,80
Remarquez que les fréquences doivent être corrigées par rpport à l’amplitude habituelle a=10 et que dans ce cas la classe modale reste toujours représentée par la 1° classe égale à [0-15[.
n termes d’interprétations on dira que la majorité de la population masculine a un âge d’environ 14 ans.
·Sachant les femmes:

On aura donc l’âge moyen et l’âge modal donnés par:
8292=x/3=
i=1
L’âge moyen dans cette population sachant qu’il s’agit des femmes, sera donc d’environ 27 ans.
Pour le mode et après correction des fréquences on peut remarquer que la distribution devient bi-modale vu que les deux classes [0-15[ et[15-25[ ont toutes les deux la plus grande fréquence F=f2/F=0,21.
D’où les deux modes suivants :
=0+15.7(0,21-0)+(0,21-0,21)
(0,21-0) =1
(0,21-0,21) =1(0,21-0,21)+(0,21-0,15)
Les deux modes sont donc égaux.
On dira que la majorité de la population féminine a un âge d’environ 15 ans.
4. Montrer que l’âge moyen national est égal à la moyenne des âges des hommes et des femmes revient à montrer que la moyenne marginale de X est égale à la moyenne des moyennes conditionnelles de X.
On doit donc vérifier si :
= F
x=
xx53
j=M
Or, la moyenne marginale de X est égale à:
D’où le tableau des statistiques marginales de X suivant:


On peut dire donne que l’âge moyen dans cette population est égal a environ 26 ans et ce quelque soit le sexe.
Alors que la moyenne des moyennes conditionnelles de X est donnée par:
F
(xx ».)+(« ‘xx ».)=xxy3
(=xx ».1+(« =xx ».)=xx’1}
/N=/
D’où:
=(0,49×25,81)+(0,51×26,78)=26,30
On en conclu ainsi que l’âge moyen national dans cette population e égal à la moyenne des âges des hommes et des femmes en même temps.
5.Le degré de dispersion de l’âge doit être vérifié en utilisant p exemple la notion de l’ET calculé pour les deux catégories H et F.
On complète ainsi les tableaux statistiques conditionnels :

On aura donc ET de l’âge sachant qu’il s’agit des hommes donné par:
imxc2-(5=M)=997,21-(25,81)=18.21
Ce qui signifie que l’âge de chaque homme pris parmi le total des hommes s’éloigne de l’âge moyen des hommes dans cette population d’environ 18 ans.
·Sachant les femmes:


D’où l’ET de l’âge sachant qu’il s’agit des femmes donné par :
Oj=F= fuFxc2-(r=)=1043,06-(26,78)2=18,06 i=1
Ce qui signifie que l’âge de chaque femme prise parmi le total des femmes s’éloigne de l’âge moyen des femmes dans cette population d’environ 18 ans.
On peut en conclure que l’âge dans cette population s’éloigne pratiquement de la même manière que se soit chez les hommes ou chez
pour des âges moyen d’environ 2 ans.
I’intervalle inter-quartile donné par qi et q3. Avce les quartiles suivants en termes de fréquences:
0.25-F-1Merg3=10+a0,75-FM
D’où les fréquences cumulées croissantes suivantes:
·Sachant les hommes:


ce qui signifie que 50% des femmes qui sont exactement au contre de cette population ont un âge inférieur à 38,85 ans et supérieure a 11,72 ans.
Ces résultats confirment en quelque sorte la conclusion précédente sur l’éloignement d’âge fait pratiquement de la même manière que se soit chez les hommes ou chez les femmes.
7.L’étendu qui englobe 80% des observations centrales doit correspondre cette fois-ci à l’intervalle limité par les déciles di et d, en laissant exactement 20% des observations répartie égalitairement à droite et à gauche çàd 10% à droite de d’y et 10% à gauche de di.
Avec:
d=10+/a.
On peut vérifier, en effet, avec les fréquences cumulées croissantes suivantes que:
Pour les hommes:
0+9=1 =4,29
d,=10+a.090- =45+(15.0290-0.83=55,5
Ce qui signifie que 80% des hommes qui sont exactement au centre de cette population ont un âge inférieur à 55,50 ans et supérieur à 4,29 ans.
Pour les femmes:
d1=10+a =4,69
+= 0,90-F1-1:F =45+15.0.90-0.83=55,5
Ce qui signifie aussi que 80% des femmes qui sont exactement au centre de cette population ont un âge inférieur à 55,50 ans et supérieur à 4,6 ans.
On voit que ces résultats confirment l’existence d’une dispersion d’âge pareille çàd presque similaire pour les hommes ainsi que pour les femmes
Exercice n° 2:
X:represente les distances parcourues par les cadres (en Km).
C’est une variable quantitative discrète puisqu’elle est représentée par des valeurs entières.
Y:représente l’âge de chacun des cadres (en années).
C’est donc une variable quantitative continue.
La population est donnée par les 44 cadres exerçant dans cette entreprise.
1.La distance marginale de X est donnée par le tableau suivant :

C’est la distribution qui représente la population composée par les 4 cadres mais en utilisant seulement les modalités de X et donc e négligeant la variable Y.
Pour la moyenne on a:
Mnj.xx;
i=1 403=9,16
=
n.. 44
Chaque cadre pris parmi les 44 observés dans cette entreprise parcou une distance moyenne de 9,16 km et ce indépendamment de son âge.
marginale de celle-ci puis on utilise l’équation de la moyenne arithmétique.

D’où, la moyenne donnée par :
て 1270=28,86
=!
y= n..
44
Indépendamment de la distance parcourue par les 44 cadres observés, leur âge moyen est d’environ 29 ans.
3. Par définition on a:
X2: la moyenne de X conditionnée par la 2° modalité de Y çàd la distance moyenne mais sachant que l’âge soit compris entre 25 et 30 ans. ý3: la moyenne de Yconditionnée par la 3° modalité de X çàd l’âge moyen mais sachant que la distance soit égale à 10 km.
D’où les tableaux statistiques suivants :
Pour X:


La moyenne sera donc égale à:
Mn12 ‘xx
xj=2 = i=1 136 =9,71
n.2 14
Chaque cadre pris parmi les 14 observés et dont l’âge est compris entre 25 et 30 ans, parcours une distance moyenne d’environ 9,71 km.
·Pour Y

Sachant que la distance parcourue par les 15 cadres observés est égale à 10 km, l’äge moyen de ces derniers est d’environ 27,5 ans.
4.On peut aisément vérifier que ces données figurant dans la 2° colonne du tableau représentent les 4 moyennes conditionnelles de Y calculées respectivement par rapport aux 4 modalités de X çàd n; X2; Est X4.

5.Oui les deux variables Y(L’âge) et X (la distance parcourue) sont dépendantes puisque les fréquences marginales ne sont pas égales aux fréquences conditionnelles. En effet, on a par exemple:
/o=/=1/9=0.1111 alors que /=/=3/4=0.1136
On peut aussi le justifier par le résultat de la question précédente. Puisque les moyennes conditionnelles changent de valeur cela signifie que la condition prise au préalable influence ce résultat et donc la variable X apporte un effet sur la variable Y. Elles sont donc dépendantes.