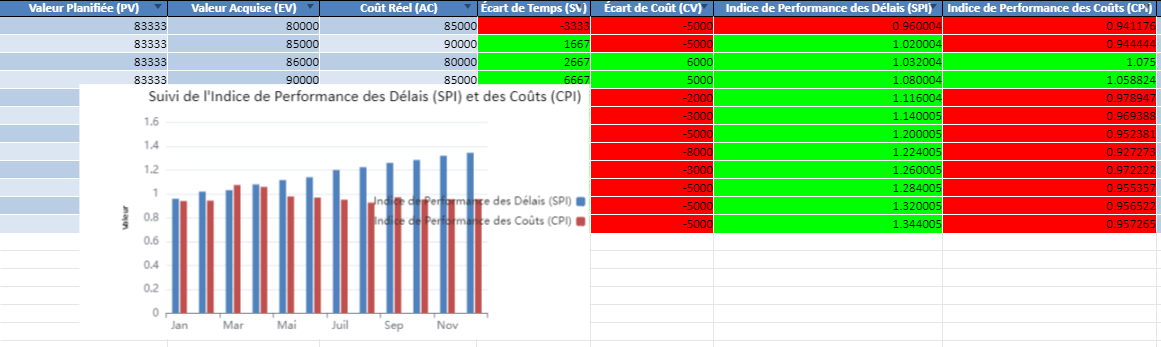
Série d’Exercices Corrigés : Analyse des Délais
Recommandés
Exercice 1 : Identification des Tâches Critiques (Chemin Critique)
Énoncé
Un projet comporte les tâches suivantes avec leurs durées et relations de dépendance. Identifiez le chemin critique en calculant les marges et la durée totale du projet.
| Tâche | Durée (jours) | Prédécesseurs |
|---|---|---|
| A | 3 | – |
| B | 5 | A |
| C | 2 | A |
| D | 4 | B |
| E | 6 | C |
| F | 3 | D, E |
Solution
Étape 1 : Dessiner le diagramme réseau
Relations entre tâches :
- A → B → D → F
- A → C → E → F
Étape 2 : Analyse avant-arrière
- Dates au plus tôt :
- A : Début 0, Fin 3.
- B : Début 3, Fin 8.
- C : Début 3, Fin 5.
- D : Début 8, Fin 12.
- E : Début 5, Fin 11.
- F : Début 12, Fin 15.
- Dates au plus tard :
- F : Début 12, Fin 15.
- D : Début 8, Fin 12.
- E : Début 5, Fin 11.
- C : Début 3, Fin 5.
- B : Début 3, Fin 8.
- A : Début 0, Fin 3.
Étape 3 : Calcul des marges
- A : Finauplustard−Finauplusto^t=3−3=0Fin au plus tard – Fin au plus tôt = 3 – 3 = 0 (critique).
- B : 8−8=08 – 8 = 0 (critique).
- C : 5−5=05 – 5 = 0.
- D : 12−12=012 – 12 = 0 (critique).
- E : 11−11=011 – 11 = 0.
- F : 15−15=015 – 15 = 0 (critique).
Chemin critique : A → B → D → F
Durée totale du projet : 15 jours.
Exercice 2 : Analyse des Écarts
Énoncé
Voici les tâches d’un projet avec les durées planifiées et les durées réelles :
| Tâche | Durée planifiée (jours) | Durée réelle (jours) | Écart (jours) |
|---|---|---|---|
| A | 3 | 4 | ? |
| B | 5 | 6 | ? |
| C | 2 | 2 | ? |
| D | 4 | 5 | ? |
- Complétez la colonne Écart.
- Analysez l’impact des écarts sur la durée totale du projet si les tâches A, B, et D sont critiques.
Solution
Étape 1 : Calcul des écarts
Eˊcart=Dureˊereˊelle−DureˊeplanifieˊeÉcart = Durée réelle – Durée planifiée
| Tâche | Durée planifiée | Durée réelle | Écart |
|---|---|---|---|
| A | 3 | 4 | 4−3=14 – 3 = 1 |
| B | 5 | 6 | 6−5=16 – 5 = 1 |
| C | 2 | 2 | 2−2=02 – 2 = 0 |
| D | 4 | 5 | 5−4=15 – 4 = 1 |
Étape 2 : Analyse de l’impact sur le projet
Si A, B, et D sont sur le chemin critique, l’impact total des écarts sur la durée du projet est la somme des écarts critiques :
1+1+1=31 + 1 + 1 = 3 jours.
Nouvelle durée totale du projet : 15+3=1815 + 3 = 18 jours.
Exercice 3 : Gestion des Retards et Ajustements Nécessaires
Énoncé
Lors d’un projet, un retard est constaté sur les tâches critiques. Voici la situation actuelle :
| Tâche | Durée réelle (jours) | Durée restante (jours) | Statut |
|---|---|---|---|
| A | 4 | – | Terminé |
| B | 6 | 1 | En cours |
| C | 3 | – | Terminé |
| D | 0 | 4 | Non commencé |
| F | 0 | 3 | Non commencé |
Proposez des ajustements pour réduire le retard.
Solution
Étape 1 : Identifier les retards critiques
Les tâches critiques (A → B → D → F) accusent un retard.
B a un retard de 1 jour et D n’a pas encore commencé.
Étape 2 : Options d’ajustement
- Compression des délais (Crashing) :
- Allouer des ressources supplémentaires à B et D pour accélérer leur exécution.
- Exemple : Réduire la durée de D de 4 à 3 jours en ajoutant un développeur.
- Chevauchement des tâches (Fast Tracking) :
- Démarrer F avant la fin de D, en supposant que certaines parties de D suffisent pour commencer F.
- Repriorisation :
- Reporter les tâches non critiques pour libérer des ressources.
Étape 3 : Résultat attendu
Avec les ajustements :
- D passe à 3 jours.
- F commence avec un jour d’avance.
Nouvelle durée totale après ajustements : 15 jours.
Résumé des apprentissages
- Identification des tâches critiques : Utilisez des marges et un diagramme réseau.
- Analyse des écarts : Comparez les durées réelles et planifiées pour évaluer les impacts.
- Gestion des retards : Appliquez des techniques comme la compression et le chevauchement pour rattraper les délais.
Suite : Analyse des Délais – Cas Particuliers et Scénarios Avancés
Cette section propose des cas particuliers qui complexifient l’analyse des délais, avec des scénarios typiques rencontrés en gestion de projet. Chaque cas inclut une situation, des données spécifiques, et une solution pour approfondir vos compétences.
Cas 1 : Tâches parallèles avec des dépendances complexes
Énoncé
Un projet comporte des tâches avec des dépendances partiellement parallèles. Voici les données :
| Tâche | Durée (jours) | Prédécesseurs | Dépendances spécifiques |
|---|---|---|---|
| A | 4 | – | – |
| B | 6 | A | Début-A-Début |
| C | 5 | A | Fin-A-Début |
| D | 3 | B | Fin-B-Début, Fin-C-Début |
- Identifiez le chemin critique en tenant compte des dépendances.
- Déterminez la durée totale du projet.
Solution
Étape 1 : Analyse des dépendances
- A doit commencer avant B et C.
- C doit finir avant que D ne commence.
- D dépend de la fin de B et C.
Étape 2 : Identification des dates au plus tôt et au plus tard
- A : Début 0, Fin 4.
- B : Début 4, Fin 10 (car dépend de Début-A-Début).
- C : Début 4, Fin 9 (car dépend de Fin-A-Début).
- D : Début 10, Fin 13 (dépend des fins de B et C).
Durée totale du projet : 13 jours. Chemin critique : A → C → D.
Cas 2 : Gestion des imprévus
Énoncé
Un imprévu survient au milieu du projet, retardant une tâche critique et augmentant sa durée. Voici la situation :
| Tâche | Durée initiale (jours) | Durée réelle (jours) | Écart (jours) | Chemin Critique |
|---|---|---|---|---|
| A | 3 | 3 | 0 | Oui |
| B | 5 | 6 | 1 | Oui |
| C | 4 | 4 | 0 | Non |
| D | 6 | 8 | 2 | Oui |
- Calculez l’impact du retard sur la durée totale.
- Proposez une stratégie pour compenser ce retard.
Solution
Étape 1 : Calcul de l’impact
- Le chemin critique est A → B → D.
- Le retard total est de 1+2=31 + 2 = 3 jours.
- Nouvelle durée totale : Dureˊeinitiale+Retard=14+3=17Durée initiale + Retard = 14 + 3 = 17 jours.
Étape 2 : Stratégies d’ajustement
- Compression des délais :
- Accélérer B ou D en ajoutant des ressources.
- Chevauchement des tâches :
- Permettre à D de commencer avant que B ne soit complètement terminé.
- Repriorisation :
- Reporter une tâche non critique pour libérer des ressources pour B ou D.
Cas 3 : Inclusion des marges dans l’analyse
Énoncé
Un projet comporte des tâches non critiques avec des marges importantes. Comment utiliser ces marges pour optimiser les ressources ?
| Tâche | Durée (jours) | Marge totale (jours) | Critique |
|---|---|---|---|
| A | 3 | 0 | Oui |
| B | 5 | 0 | Oui |
| C | 4 | 2 | Non |
| D | 6 | 1 | Non |
- Identifiez les tâches qui peuvent être retardées sans impacter le projet.
- Proposez une réallocation des ressources pour maximiser l’efficacité.
Solution
Étape 1 : Identification des marges utilisables
- Tâche C a une marge de 2 jours.
- Tâche D a une marge de 1 jour.
Étape 2 : Optimisation des ressources
- Reporter une partie des efforts de C et D pour renforcer les ressources sur A ou B, qui sont critiques.
- Réduire les effectifs sur C pour permettre une allocation sur D si nécessaire.
Cas 4 : Analyse des retards en série
Énoncé
Un projet est affecté par des retards cumulés sur plusieurs tâches non critiques, créant un impact sur les tâches critiques.
| Tâche | Durée initiale (jours) | Durée réelle (jours) | Critique |
|---|---|---|---|
| A | 3 | 3 | Oui |
| B | 5 | 5 | Oui |
| C | 4 | 6 | Non |
| D | 6 | 8 | Non |
- Évaluez si les retards sur C et D affectent le projet.
- Déterminez si une tâche non critique devient critique après le retard.
Solution
Étape 1 : Impact des retards sur C et D
- Nouvelle durée de C : 6 jours, marge utilisée : 6−4=26 – 4 = 2 jours.
- Nouvelle durée de D : 8 jours, dépasse la marge (impact sur le projet critique).
Étape 2 : Recalcul des marges
- Si les retards sur D dépassent la marge, D devient critique.
Étape 3 : Ajustement
- Allouer des ressources supplémentaires pour réduire la durée de D.
- Réévaluer le chemin critique pour inclure D.
Conclusion
Ces cas particuliers mettent en évidence des scénarios avancés :
- Les dépendances parallèles et complexes.
- La gestion des imprévus et retards.
- L’optimisation des marges pour une meilleure allocation des ressources.
- La requalification des tâches non critiques en tâches critiques en fonction des retards.