statistique descriptive- Application séries chronologiques
Recommandés
Bienvenue dans ce cours statistique descriptive – Application des séries chronologiques
Lire le chapitre précédent Statistique: LES APPLICATIONS DES SERIES CHRONOLOGIQUES
Application statistiques descriptives




on constate, en effet, que la courbe représentant la série par la MMA prend pratiquement la forme d’une ligne. Ce qui justifie la suppression des effets indésirables tels que les éléments de perturbations résiduels et
on peut éventuellement donner le graphe ci-dessous dans lequel on peut comparer le résultat du lissage effectué par les MM-4(t) vis-à-vis de celui donné par les autres moyennes MMp-3(t) et MMp-s(t). Ces derniers montrent visiblement la persistence des éléments saisonniers et résiduels.
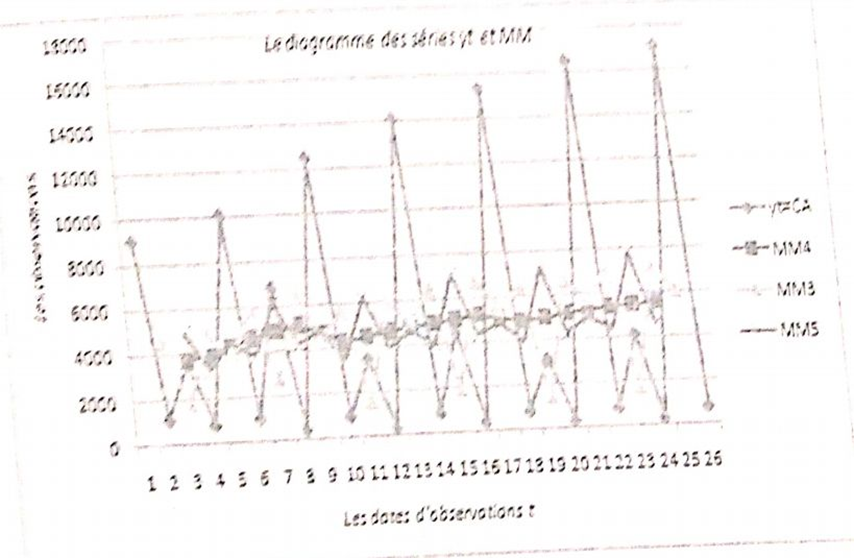
On montre ainsi que le meilleur résultat est celui effectué par la MMp-4(t) dont l’ordre correspond à la périodicité p=4.
-La dessaisonalisation en utilisant une des méthodes de lisage détermination du trend.
-a méthode du 《rapport au trend » pour l’estimation des variations cycliques.
-Et la méthode des 《CS” afin d’estimer les variations saisonnières.
Les résultats correspondants aux deux premières étapes sont récapitulés dans le tableau suivant:


ce qui nous permet d’avoir les résultats de la 3° méthode des CS qui sont capitulés par trimestres dans le tableau suivant:

Les moyennes par trimestres de l’avant dernière ligne du tableau ci-dessus (Moy/tr) sont déterminées en calculant la somme des coefficients saisonniers par colonne çàd par trimestre et en la divisant par le nombre des mêmes coefficients. Bien entendu, les 3 premiers coefficients de l’année 2003 et les 3 derniers de l’année 2009 ne sont pas disponibles.
Enfin, on trouve dans la dernière ligne les CSA Coefficients Saisonniers Ajustés qui nous servirons de coefficients d’estimation pour la variable d’intérêt notamment le chiffre d’affaire dans ce cas. On en conclu, par conséquent, que seul le deuxième trimestre qui correspond à la haute saison alors que les trimestres 1, 3 et 4 correspondent par contre à la basse saison.
4. Afin de calculer le CA prévisionnel du 4° trimestre de l’année 2011 il-faut trouver l’équation d’estimation (càd de régression linéaire) et utiliser le CSA correspondant et donné dans la question précédente.
Les résultats sont repris comme suit:



Avec:
T=4950,54 et t=13,5
A=0 =5632,67 et σ,=2-(i)=7,5
cov(T,t)=T.t-T.t=2947,02
Les CA sont liés positivement au temps.
—– Application des séries chronologiques—–
les CA de cette entreprise augmentent aussi.
b=T-â1=4243,26
ce qui représente le niveau constant des CA indépendamment du
temps.
L’équation du trend donnée par le modéle linéaire sera présentée ainsi:
y1=T=at+b
=52,39.t+4243,26
Malheureusement, cette équation n’est pas bonne pour en faire des prévisions sures vu que le coefficient de corrélation est trop faible de l’ordre seulement de 7%. Ce qui affaiblit énormément la qualité de la
prévision.
Si on néglige cette dernière information sur la qualité de la prévision, le chiffre d’affaire à prévoir pour le 4° trimestre de l’année 2011 sera calculé avec:
*La date: t=26+1+4+4=35
Le 4° trimestre doit correspondre à:
1:représente le 4° trimestre de l’année 2009.
4:représente les 4 trimestres de l’année 2010.
1:représente les 4 trimestres de l’année 2011.
*Prévision:
y1=T=(ât+b)xCSA
t=4° trimestre
CA1=35=((52,39*35)+4243,26)*0,8962
=5446,13 en um.
Le CA qui sera prévu pour cette entreprise pour le 4° trimestre en 2011 sera de 5446,13 u.m. C’est un chiffre qui prend en considération la correction des événements de perturbations et des effets saisonniers vu qu’on utilise ici le CSA. Cependant, il faut faire attention tout de même à la faiblesse de la prévision(R=7%).
Exercice n° 5:
serie chronologique dans cette application est représentée par les La notations mensuelles réalisées pour la période allant de 200 2010.Nous avons un total de 36 données mensuelles.
1.La représentation graphique de la série est donnée par :

2. On constate que le modèle de décomposition est additif étant donné que l’amplitude entre les extremums reste constante. La série brute y, présente également beaucoup de variations anormales notamment saisonnières, cycliques et accidentelles.
3.Le lissage de la série brute en utilisant la MM3 et la méthode exponentielle pour un coefficient α=0,1 est reformulé dans le tableau suivant:




Comme on peut le constater, la première et la dernière valeur dans la colon
ne de MM3 sont inexistantes alors que du côté de LE on garde la
Exponentiel par rapport à la Moyenne Mobile en général.
D’où le graph suivant:
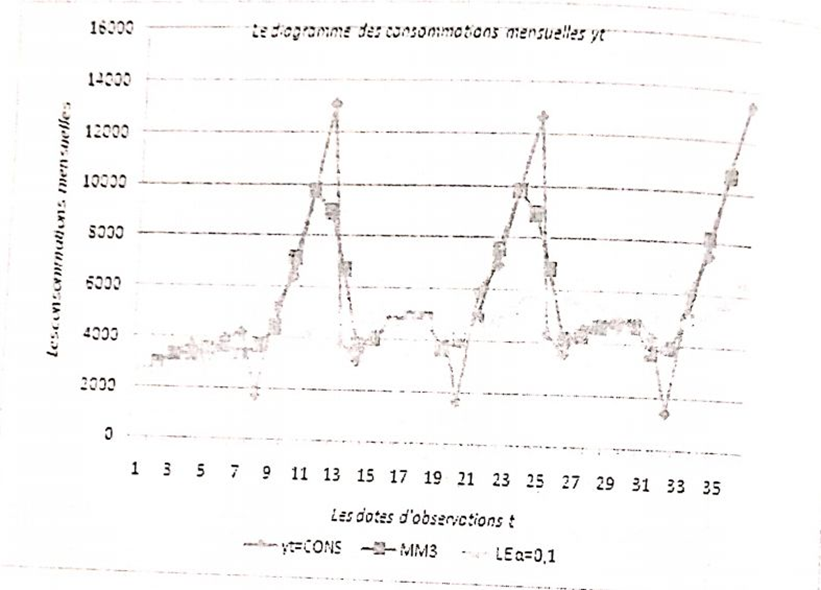
Comme on peut le remarquer sur le graphe le lissage par MM3 ne permet pas d’avoir une bonne déssaisonnalisation vu que la série obtenue garde beaucoup de variations saisonnières et accidentelles. Par contre, le lissage exponentiel permet de nettoyer la série brute de ces variations non normales.
NB. On peut éventuellement montrer que les MM d’ordre 4 et d’ordre 5 ne permettent pas non plus d’avoir un bon lissage.
5. L’estimation des différentes variations de trend, de variations cycliques et de variations saisonnières doit être faite en respectant les normes et les étapes définies pour chacune de ces mouvements.
On va classer dans ce qui suit les différentes estimations selon leurs principes, tels que:
pour le résultat de cette étape est donné dans le tableau précédent dans la question précédente aussi.
L’estimation des variations cycliques:
Elle sera faite en calculant :
– le trend prévisionnel estimé par la bonne méthode de dessaisonalisation donnée telle que, la MM ou même la DRL. Dans notre cas on opte pour la même raison précitée pour le α=0,1.
– la différence entre la série brute y, et le trend prévisionnel selon la méthode d’estimation. Dans notre cas aussi il faut retrancher le résultat du LE α=0,1 de la série brute yi.
Les résultats de l’estimation des variations cycliques sont donnés comme suit:




On peut clairement voir sur le graphe suivant:

On constate ainsi que les «différences au trend» données par (V:-LE) se situent au-dessus et en-dessous de la droite du trend. Ce qui signifie que les variations sont beaucoup plus accidentelles (les variations passent à travers le trend) et pas cycliques.
L’estimation des variations saisonnières :
L’estimation des variations saisonnières sera faite en calculant :
-la série désaisonnalisée par LE (le résultat 5.1.)
– la différence par mois entre la série brute y, et la série lissée par LE(le résultat 5.2.).
– les moyennes par mois. -l’ajustement des moyennes en divisant par le total des moyennes
et en multipliant par le mouvement saisonnier p=12.
D’où les résultats suivants:


Les moyennes par mois de l’avant dernière colonne (Moy/tr) sont
déterminées en calculant la somme des coefficients saisonniers par ligne
çàd par mois et en la divisant par le nombre des mêmes coefficients.
La dernière colonne présente les CSA Coefficients Saisonniers Ajustés qui
nous servirons de coefficients d’estimation pour la variable d’intérêt yy.
Par ailleurs, tous les mois dont la valeur du CSA est supérieure à l
correspondront à la haute saison alors que les mois dont la valeur du
CSA est inférieure à l correspondront par contre à la basse saison.
6. Afin de calculer la consommation mensuelle prévisionnelle du 6° mois de l’année 2011 on donne d’abord l’équation servant d’estimation (la régression linéaire) en supposant en fait que le trend évolue linéairement.
Les résultats sont repris comme suit:




Avec:
〒=5518,89 et t=18,5
〒 -(テ) = 3096,73 et σ, =/2-(E}=10,39
cov(T,t)=T.t-T1=11346,37
ā=cCov(7.0)=105.14
b=T-at=3573,86
L’équation du trend donnée par le modèle linéaire sera présentée ainsi:
y1=T=ât+b
=105,14.t+3573,86
Malheureusement, cette équation n’est pas assez bonne pour en faire des prévisions sures vu que le coefficient de corrélation est relativement faible de l’ordre de 35%. Ce qui risque de baisser la qualité de la prévision.
Si on néglige cette dernière information sur la qualité de la prévision, le chiffre d’affaire à prévoir pour le 6° mois de l’année 2011 sera calculé avec:
*La date:
Le 6° mois de l’an 2011 doit correspondre à: t=36+6=42
36 : représente les observations disponibles de 2009 à 2010.
6:représente les 6premiers mois de l’année 2011.
*Prévision:
y1=T=(ât+b)xCSA1=6mois
Consi=42 = ((105,14*42)+3573,86)*0,3695
=2952,2089 en um.
La consommation qui sera prévue pour cette entreprise pour le 6° mois de 2011 sera de 2952,2089 en u.m. C’est un chiffre qui prend en considération la correction des événements de perturbations et des effets saisonniers mais avec une faiblesse de précision étant donné que le R est seulement de 4%.