Parité d’une Fonction : Exercices Corrigés
Recommandés
La parité d’une fonction est un concept fondamental en mathématiques qui permet de caractériser le comportement de la fonction en rapport avec la symétrie de son graphe. Une fonction peut être soit paire, soit impaire, soit ni l’une ni l’autre. Dans cet article, nous allons explorer ces concepts à travers des exercices corrigés pour mieux comprendre leur application.
Définition
- Fonction paire : Une fonction ( f ) est dite paire si pour tout ( x ) dans son domaine, ( f(-x) = f(x) ). Le graphe d’une fonction paire est symétrique par rapport à l’axe des ordonnées (axe vertical).
- Fonction impaire : Une fonction ( f ) est dite impaire si pour tout ( x ) dans son domaine, ( f(-x) = -f(x) ). Le graphe d’une fonction impaire est symétrique par rapport à l’origine.
Exercices Corrigés
Exercice 1 : Identifier la Parité d’une Fonction
Énoncé : Déterminer si la fonction suivante est paire, impaire ou ni l’une ni l’autre.
[ f(x) = x^2 + 3 ]
Correction :
- Calculons ( f(-x) ) :
[ f(-x) = (-x)^2 + 3 = x^2 + 3 ] - Comparons ( f(-x) ) à ( f(x) ) :
[ f(-x) = f(x) ]
La fonction ( f(x) = x^2 + 3 ) est donc paire.
Exercice 2 : Identifier la Parité d’une Fonction
Énoncé : Déterminer si la fonction suivante est paire, impaire ou ni l’une ni l’autre.
[ g(x) = x^3 – x ]
Correction :
- Calculons ( g(-x) ) :
[ g(-x) = (-x)^3 – (-x) = -x^3 + x ] - Comparons ( g(-x) ) à ( -g(x) ) :
[ -g(x) = -(x^3 – x) = -x^3 + x ]
[ g(-x) = -g(x) ]
La fonction ( g(x) = x^3 – x ) est donc impaire.
Exercice 3 : Analyser la Parité d’une Fonction Composée
Énoncé : Déterminer si la fonction suivante est paire, impaire ou ni l’une ni l’autre.
[ h(x) = x^2 + x ]
Correction :
Calculons:
h(−x)=(−x)2+(−x)=x2−x
La fonction ( h(x) = x^2 + x ) n’est ni paire ni impaire.

Parité d’une Fonction : Exercices Avancés Corrigés
Après avoir abordé les bases de la parité des fonctions, nous allons maintenant explorer des exercices plus avancés. Ces exercices nécessitent une compréhension approfondie des concepts de parité et peuvent impliquer des opérations sur des fonctions plus complexes.
Exercices Avancés
Exercice 1 : Composition et Parité
Énoncé : Soient les fonctions ( f(x) = x^3 ) et ( g(x) = \cos(x) ). Déterminer la parité de la fonction composée ( h(x) = f(g(x)) ).
Correction :
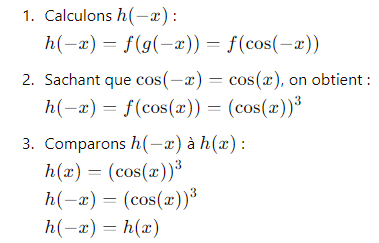
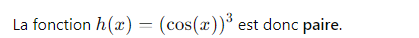
Exercice 2 : Parité et Dérivées
Énoncé : Soit la fonction ( f(x) = e^{-x^2} ). Déterminer si sa dérivée ( f'(x) ) est paire, impaire ou ni l’une ni l’autre.
Correction :
- Calculons la dérivée ( f'(x) ) :
[ f(x) = e^{-x^2} ]
[ f'(x) = \frac{d}{dx} (e^{-x^2}) = -2x e^{-x^2} ] - Calculons ( f'(-x) ) :
[ f'(-x) = -2(-x) e^{-(-x)^2} = 2x e^{-x^2} ] - Comparons ( f'(-x) ) à ( f'(x) ) et ( -f'(x) ) :
[ f'(-x) = -f'(x) ]
La dérivée ( f'(x) = -2x e^{-x^2} ) est donc impaire.
Exercice 3 : Parité d’une Fonction Définie par Morceaux
Énoncé : Soit la fonction définie par morceaux suivante :
Déterminer si cette fonction est paire, impaire ou ni l’une ni l’autre.
Correction :
- Calculons ( f(-x) ) pour ( x \geq 0 ) :
[ f(-x) = f(x) = x^2 – 1 ] - Calculons ( f(-x) ) pour ( x < 0 ) :
[ f(-x) = f(-x) = 1 – (-x)^2 = 1 – x^2 ] - Comparons les deux résultats :
Pour ( x \geq 0 ) :
[ f(-x) = x^2 – 1 ]
[ f(x) = x^2 – 1 ]
Pour ( x < 0 ) :
[ f(-x) = 1 – x^2 ]
[ f(x) = 1 – x^2 ]
Dans les deux cas, ( f(-x) = f(x) ).
La fonction définie par morceaux est donc paire.
Exercice 4 : Parité d’une Fonction Trigonométrique Composée
Énoncé : Soit la fonction ( f(x) = \sin(x^2) ). Déterminer si cette fonction est paire, impaire ou ni l’une ni l’autre.
Correction :
- Calculons ( f(-x) ) :
[ f(-x) = \sin((-x)^2) = \sin(x^2) ] - Comparons ( f(-x) ) à ( f(x) ) :
[ f(-x) = f(x) ]
La fonction ( f(x) = \sin(x^2) ) est donc paire.
Conclusion
La parité des fonctions est un concept clé pour comprendre la symétrie des graphes des fonctions. En identifiant si une fonction est paire, impaire ou ni l’une ni l’autre, nous pouvons mieux appréhender leur comportement et leurs propriétés. Les exercices corrigés ci-dessus montrent comment aborder et résoudre des problèmes de parité de fonctions de manière méthodique.