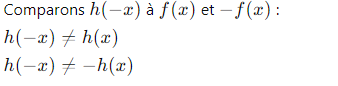La Parité d’une Fonction : Utilisation et Importance

En mathématiques, la parité d’une fonction est un concept qui aide à comprendre la symétrie des fonctions par rapport à l’axe vertical. Une fonction peut être paire, impaire, ou ni l’un ni l’autre. Ce concept a des applications pratiques dans diverses branches des mathématiques et des sciences appliquées. Cet article explore la définition de la parité d’une fonction, ses propriétés, et ses utilisations.

Définition

Fonction Paire

Une fonction ( f(x) ) est dite paire si elle satisfait la condition suivante pour tous les ( x ) dans le domaine de ( f ) :
[ f(-x) = f(x) ]

Graphiquement, cela signifie que la courbe de la fonction est symétrique par rapport à l’axe vertical (l’axe des ordonnées).

Fonction Impaire

Une fonction ( f(x) ) est dite impaire si elle satisfait la condition suivante pour tous les ( x ) dans le domaine de ( f ) :
[ f(-x) = -f(x) ]

Graphiquement, cela signifie que la courbe de la fonction est symétrique par rapport à l’origine.

Exemple de Fonctions

• Fonction Paire : ( f(x) = x^2 )
• Fonction Impaire : ( f(x) = x^3 )
• Ni Paire ni Impaire : ( f(x) = x^2 + x )

Propriétés

Combinaison de Fonctions :

• La somme de deux fonctions paires est une fonction paire.
• La somme de deux fonctions impaires est une fonction impaire.
• La somme d’une fonction paire et d’une fonction impaire n’est ni paire ni impaire.

Produit de Fonctions :

• Le produit de deux fonctions paires est une fonction paire.
• Le produit de deux fonctions impaires est une fonction paire.
• Le produit d’une fonction paire et d’une fonction impaire est une fonction impaire.

Composition de Fonctions :

• La composition de deux fonctions paires est paire.
• La composition de deux fonctions impaires est impaire.
• La composition d’une fonction paire et d’une fonction impaire n’est ni paire ni impaire.

Utilisation

1. Analyse et Résolution d’Équations Différentielles

La parité des fonctions joue un rôle crucial dans la simplification et la résolution d’équations différentielles. Par exemple, dans la résolution des équations de type Fourier, les fonctions paires et impaires peuvent être traitées séparément pour simplifier le processus de transformation.

2. Physique et Ingénierie

En physique, de nombreuses lois et phénomènes naturels présentent des symétries qui peuvent être modélisées par des fonctions paires ou impaires. Par exemple, le potentiel électrique d’une charge placée à l’origine est une fonction paire.

3. Analyse des Séries de Fourier

Lors de l’analyse des séries de Fourier, les fonctions paires et impaires facilitent la décomposition en séries de cosinus (pour les fonctions paires) et en séries de sinus (pour les fonctions impaires). Cela permet de simplifier les calculs et d’analyser les signaux périodiques de manière plus efficace.

4. Traitement du Signal

En traitement du signal, les propriétés de parité sont utilisées pour analyser et traiter les signaux symétriques. Les systèmes linéaires et les filtres peuvent exploiter cette symétrie pour améliorer les performances et l’efficacité du traitement.

Cas Pratique : Analyse de la Parité d’une Fonction avec Python

Dans ce cas pratique, nous allons écrire un programme en Python pour analyser la parité d’une fonction. Nous vérifierons si une fonction donnée est paire, impaire, ou ni l’un ni l’autre en utilisant une approche numérique. Nous illustrerons cela avec des exemples concrets.

1. Définition de la Fonction à Analyser

Commençons par définir une fonction que nous voulons analyser. Par exemple, nous utiliserons ( f(x) = x^2 ) (fonction paire) et ( g(x) = x^3 ) (fonction impaire).

2. Implémentation en Python

Voici un script Python pour analyser la parité d’une fonction :

import numpy as np
import matplotlib.pyplot as plt

# Définir les fonctions
def f(x):
    return x**2

def g(x):
    return x**3

# Définir une fonction pour tester la parité
def test_parity(func, x_values):
    is_even = True
    is_odd = True

    for x in x_values:
        if func(-x) != func(x):
            is_even = False
        if func(-x) != -func(x):
            is_odd = False

    if is_even:
        return "Paire"
    elif is_odd:
        return "Impaire"
    else:
        return "Ni Paire ni Impaire"

# Générer des valeurs pour x
x_values = np.linspace(-10, 10, 400)

# Tester les fonctions
result_f = test_parity(f, x_values)
result_g = test_parity(g, x_values)

print(f"La fonction f(x) = x^2 est : {result_f}")
print(f"La fonction g(x) = x^3 est : {result_g}")

# Tracer les fonctions
plt.figure(figsize=(12, 6))

plt.subplot(1, 2, 1)
plt.plot(x_values, f(x_values), label='f(x) = x^2')
plt.title(f"f(x) = x^2 (Parité: {result_f})")
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(x_values, g(x_values), label='g(x) = x^3')
plt.title(f"g(x) = x^3 (Parité: {result_g})")
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
plt.legend()

plt.show()

3. Explication du Script

1. Définition des Fonctions : Nous définissons deux fonctions ( f(x) = x^2 ) et ( g(x) = x^3 ).
2. Test de la Parité : La fonction test_parity prend une fonction et un ensemble de valeurs ( x ). Elle vérifie si la fonction est paire, impaire, ou ni l’un ni l’autre en comparant ( f(-x) ) et ( f(x) ) pour la parité paire, et ( f(-x) ) et (-f(x) ) pour la parité impaire.
3. Génération des Valeurs de ( x ) : Nous utilisons np.linspace pour générer une plage de valeurs pour ( x ).
4. Résultat de la Parité : Nous appliquons test_parity aux fonctions ( f ) et ( g ) et affichons les résultats.
5. Visualisation : Nous utilisons matplotlib pour tracer les fonctions et illustrer leur parité.

4. Résultats

En exécutant ce script, vous obtiendrez les résultats suivants :

La fonction f(x) = x^2 est : Paire
La fonction g(x) = x^3 est : Impaire

Les graphiques générés montreront la symétrie par rapport à l’axe vertical pour ( f(x) = x^2 ) et la symétrie par rapport à l’origine pour ( g(x) = x^3 ).

Synthèse

Ce cas pratique montre comment analyser la parité d’une fonction en utilisant Python. La compréhension de la parité peut aider à simplifier des problèmes mathématiques complexes et à trouver des solutions plus élégantes. Les concepts et le code présentés ici peuvent être étendus à d’autres fonctions et contextes d’analyse.

Application Pratique : Analyse de la Parité d’une Fonction dans le Traitement des Signaux

Dans cette application, nous allons utiliser Python pour analyser la parité d’une fonction dans le cadre du traitement des signaux. Nous allons créer un signal périodique, vérifier sa parité, et utiliser cette information pour effectuer une analyse de Fourier.

Étapes de l’Application

1. Création d’un Signal Périodique.
2. Vérification de la Parité du Signal.
3. Analyse de Fourier en Utilisant les Propriétés de Parité.

1. Création d’un Signal Périodique

Nous allons créer un signal composé de plusieurs composantes sinusoïdales et cosinusoidales.

import numpy as np
import matplotlib.pyplot as plt

# Définir les paramètres du signal
t = np.linspace(-2 * np.pi, 2 * np.pi, 400)  # Période de temps
signal = np.sin(t) + 0.5 * np.cos(2 * t)  # Signal composite

# Afficher le signal
plt.plot(t, signal)
plt.title("Signal Composite")
plt.xlabel("Temps")
plt.ylabel("Amplitude")
plt.grid(True)
plt.show()

2. Vérification de la Parité du Signal

Nous allons définir une fonction pour vérifier la parité du signal.

def test_parity(func, x_values):
    is_even = True
    is_odd = True

    for x in x_values:
        if func(-x) != func(x):
            is_even = False
        if func(-x) != -func(x):
            is_odd = False

    if is_even:
        return "Paire"
    elif is_odd:
        return "Impaire"
    else:
        return "Ni Paire ni Impaire"

# Définir le signal comme une fonction
def signal_function(x):
    return np.sin(x) + 0.5 * np.cos(2 * x)

# Tester la parité du signal
x_values = np.linspace(-2 * np.pi, 2 * np.pi, 400)
parity_result = test_parity(signal_function, x_values)
print(f"Le signal est : {parity_result}")

3. Analyse de Fourier en Utilisant les Propriétés de Parité

Nous allons effectuer une transformée de Fourier discrète (DFT) pour analyser le spectre fréquentiel du signal.

from scipy.fft import fft, fftfreq

# Effectuer la transformée de Fourier
N = len(t)
yf = fft(signal)
xf = fftfreq(N, (t[1] - t[0]) / (2.0 * np.pi))  # Fréquences

# Tracer le spectre de Fourier
plt.plot(xf, np.abs(yf))
plt.title("Spectre de Fourier du Signal Composite")
plt.xlabel("Fréquence (rad/s)")
plt.ylabel("Amplitude")
plt.grid(True)
plt.show()

Résultats

1. Parité du Signal : Le script imprimera si le signal est paire, impaire, ou ni l’un ni l’autre.
2. Spectre de Fourier : Le graphique du spectre de Fourier montrera les composantes fréquentielles du signal.

Synthèse

Cette application pratique démontre comment utiliser Python pour analyser la parité d’un signal et appliquer cette analyse dans le contexte du traitement des signaux. La connaissance de la parité peut simplifier l’analyse de Fourier, permettant de décomposer les signaux en leurs composantes fondamentales de manière plus efficace. Les concepts et le code présentés peuvent être étendus pour analyser d’autres types de signaux et applications dans le traitement des données.

Conclusion

La parité d’une fonction est un concept fondamental en mathématiques, avec des applications étendues en physique, en ingénierie, et en traitement du signal. Comprendre si une fonction est paire, impaire ou ni l’un ni l’autre peut simplifier de nombreux problèmes complexes et offrir des insights précieux dans l’analyse et la modélisation des systèmes naturels et artificiels.

En intégrant la compréhension de la parité dans les outils analytiques et les méthodes de résolution, les mathématiciens et les ingénieurs peuvent exploiter les symétries inhérentes aux fonctions pour des solutions plus élégantes et efficaces.