Comment calculer la racine carrée avec l’approximation linéaire ?

Dans ce tutoriel mathématique, on vous montre comment calculer une racine carrée avec la méthode de l’approximation linéaire.

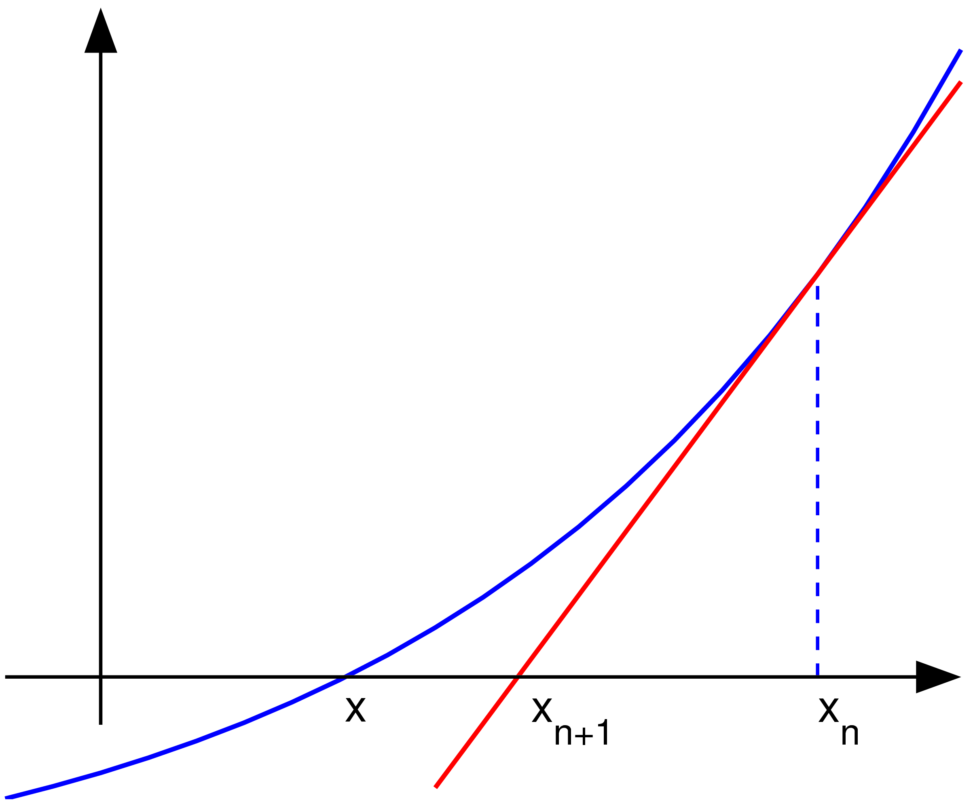
Calcul de la racine carrée en utilisant une approximation linéaire

Au lieu de recourir à des méthodes complexes pour calculer la racine carrée d’un nombre en JavaScript, il existe une approche plus simple utilisant une approximation linéaire. Cette méthode se base sur une équation linéaire :

L(x) = f(a) + f'(a)*(x-a)

Ici, “a” est choisi comme un carré parfait, et “f(a)” représente sa √. La dérivée de la fonction racine carrée est la moitié de l’inverse de la √.

Donc, l’approximation de la racine carrée devient :

sqrt_approx(x) = sqrt_int(a) + (x-a)/(2*sqrt_int(a))

Pour que cette approximation fonctionne, il faut trouver le carré parfait le plus proche de x. L’algorithme se décompose comme suit :

Trouver le carré parfait le plus proche de x.
Appliquer la formule d’approximation.

Le code JavaScript qui en découle ressemble à ceci :

function sqrt_approx(x) {
    let sqrt_a = closest_square_root(x);
    let a = sqrt_a * sqrt_a;

    return sqrt_a + (x - a) / (2 * sqrt_a);
}

Pour déterminer le carré parfait le plus proche de x, nous itérons sur des nombres entiers positifs en calculant leur carré et en vérifiant la distance par rapport à x. Lorsque la distance cesse d’être négative et devient positive, nous renvoyons soit l’élément courant de l’itération, soit l’élément précédent, selon le carré le plus proche de x. Voici le code correspondant :

function closestSquareRoot(x) {
    let i = 0;
    while (i * i < x) {
        i++;
    }
    let dist_ii = i * i - x;
    let dist_ant = x - (i - 1) * (i - 1);

    return dist_ant < dist_ii ? i - 1 : i;
}

Cette méthode simplifiée permet de calculer rapidement la √ d’un nombre en JavaScript, ce qui peut s’avérer utile dans divers contextes.

Standarisation de la méthode dans les langages de la programmation

En Python :

def closest_square_root(x):
    i = 0
    while i * i < x:
        i += 1
    dist_ii = i * i - x
    dist_ant = x - (i - 1) * (i - 1)

    return i - 1 if dist_ant < dist_ii else i

En C++ :

#include <iostream>
#include <cmath>

int closestSquareRoot(int x) {
    int i = 0;
    while (i * i < x) {
        i++;
    }
    int dist_ii = i * i - x;
    int dist_ant = x - (i - 1) * (i - 1);

    return dist_ant < dist_ii ? i - 1 : i;
}

int main() {
    int x = 25;
    int root = closestSquareRoot(x);
    std::cout << "La √ de " << x << " est " << root << std::endl;
    return 0;
}

En Java :

public class SquareRoot {
    public static int closestSquareRoot(int x) {
        int i = 0;
        while (i * i < x) {
            i++;
        }
        int distIi = i * i - x;
        int distAnt = x - (i - 1) * (i - 1);

        return distAnt < distIi ? i - 1 : i;
    }

    public static void main(String[] args) {
        int x = 25;
        int root = closestSquareRoot(x);
        System.out.println("La racine carrée de " + x + " est " + root);
    }
}

Ces exemples dans différents langages accomplissent essentiellement la même tâche : trouver le carré parfait le plus proche d’un nombre donné pour approximer la √.

Annexe

L’approximation linéaire est couramment utilisée pour estimer des fonctions complexes dans les mathématiques, la science et l’ingénierie. Elle simplifie les calculs complexes en utilisant des fonctions linéaires proches pour obtenir des résultats précis.

L’utilité de l’approximation linéaire réside dans sa capacité à rendre des problèmes mathématiques compliqués plus gérables. Elle permet de simplifier des équations et des calculs en remplaçant une fonction complexe par une droite ou un plan qui s’en rapproche, ce qui facilite l’analyse et la résolution des problèmes.

En mathématiques, l’approximation linéaire est couramment utilisée pour résoudre des équations différentielles, des problèmes d’optimisation, des interpolations de données, des simulations numériques, et bien d’autres applications. Elle permet d’obtenir des résultats rapidement, même si ces résultats ne sont que des estimations, ce qui peut être suffisant dans de nombreuses situations.

En résumé, l’approximation linéaire est une puissante technique mathématique qui simplifie des problèmes complexes en les ramenant à des formes linéaires plus faciles à manipuler, ce qui facilite la modélisation, la résolution de problèmes et la compréhension des phénomènes mathématiques et scientifiques.