Comprendre le Coefficient de Variation : Étude de Cas et Exercices Corrigés
Recommandés
Le coefficient de variation (CV) est un outil statistique puissant utilisé dans divers domaines pour évaluer la dispersion relative des données par rapport à leur moyenne. Il est particulièrement utile lorsqu’on compare des ensembles de données présentant des moyennes différentes. Dans cet article, nous allons examiner en détail le concept de coefficient de variation à travers une étude de cas et présenter des exercices corrigés pour consolider la compréhension.
Qu’est-ce que le Coefficient de Variation ?
Le CV est défini comme le rapport de l’écart type à la moyenne, exprimé en pourcentage. Mathématiquement, il est représenté comme suit :
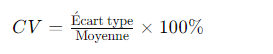
Un CV élevé indique une grande dispersion des données par rapport à la moyenne, tandis qu’un coefficient de variation faible suggère une dispersion moindre.
Étude de Cas : Utilisation du CV
Prenons l’exemple d’une entreprise qui souhaite évaluer la variabilité des performances de ses deux départements : ventes et marketing. Les données suivantes représentent les bénéfices mensuels des deux départements sur une période de douze mois :
- Département des Ventes : 10,000; 12,000; 9,500; 11,200; 10,800; 11,500; 9,700; 10,300; 11,000; 10,200; 11,400; 10,600
- Département du Marketing : 8,000; 8,200; 8,500; 8,400; 8,300; 8,700; 8,600; 8,800; 8,900; 9,000; 8,600; 9,100
Calculons d’abord les moyennes et les écarts types pour chaque département, puis déterminons leurs coefficients de variation :

Comparons maintenant les coefficients de variation des deux départements. Bien que les bénéfices moyens du département des Ventes soient plus élevés que ceux du département du Marketing, le coefficient de variation des ventes (6.13%) est également plus élevé, ce qui indique une dispersion relative plus grande des données par rapport à leur moyenne.
Exercices Corrigés
- Données : 15, 18, 20, 22, 25. Calculer le coefficient de variation.
Solution :
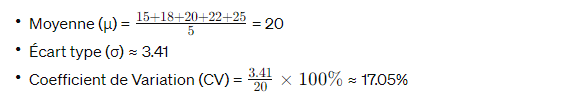
Données : 50, 55, 60, 65, 70, 75, 80, 85. Calculer le coefficient de variation.
Solution :
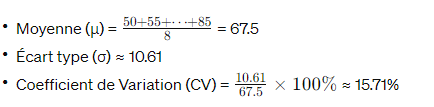
Voici une série d’exercices sur le CV avec leurs solutions :
Exercice 1 :
Les temps de réponse (en secondes) de deux systèmes informatiques sont donnés ci-dessous. Calculez le coefficient de variation pour chaque système et comparez leur variabilité.
- Système A : 3.2, 3.5, 3.1, 3.3, 3.4
- Système B : 2.9, 4.0, 3.0, 3.2, 3.5
Solution :
Pour le système A :
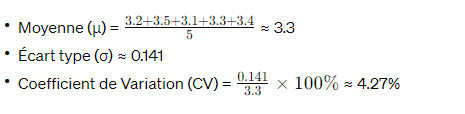
Pour le système B :
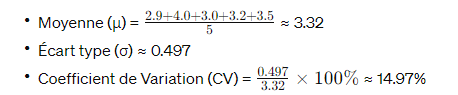
Le système B présente une variabilité plus élevée avec un CV variation plus élevé.
Exercice 2 :
Un étudiant prend des examens de mathématiques sur cinq semaines consécutives. Les scores obtenus sont les suivants : 85, 90, 88, 92, 87. Calculez le coefficient de variation pour évaluer la variabilité de ses performances.
Solution :

Exercice 3 :
Les poids (en kg) de deux groupes de personnes sont donnés ci-dessous. Calculez le CV pour chaque groupe et déterminez lequel a une dispersion relative plus élevée.
- Groupe 1 : 60, 62, 58, 65, 63
- Groupe 2 : 70, 50, 75, 55, 80
Solution :
Pour le groupe 1 :
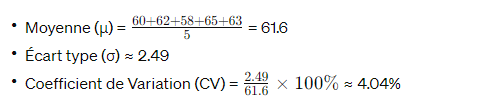
Pour le groupe 2 :
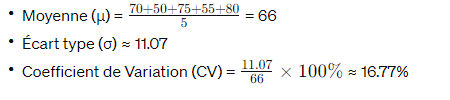
Le groupe 2 présente une dispersion relative plus élevée avec un coefficient de variation plus élevé.
Ces exercices devraient vous aider à comprendre comment calculer et interpréter le CV dans différents contextes.