Tableau d’amortissement d’un emprunt : Exercices corrigés
Recommandés
Fiche Pratique : Tableau d’Amortissement d’un Emprunt
1. Définition du Tableau d’Amortissement
Un tableau d’amortissement est un document financier qui détaille le remboursement d’un emprunt sur sa durée. Il présente, pour chaque période (mois ou année), le montant de la mensualité, la part des intérêts, l’amortissement du capital et le capital restant dû. Le tableau permet de visualiser l’évolution de l’emprunt jusqu’à son remboursement total.
2. Composants du Tableau d’Amortissement
- Mensualité : Montant fixe ou variable que l’emprunteur rembourse périodiquement (mensuellement, généralement). Elle peut inclure une part d’intérêt et une part d’amortissement.
- Intérêt : Part de la mensualité correspondant aux frais d’emprunt. Calculé sur le capital restant dû.
- Amortissement : Part de la mensualité qui sert à rembourser le capital emprunté.
- Capital Restant Dû : Montant du capital qui reste à rembourser après chaque paiement.
3. Types de Remboursement
- Amortissement Constant : Le capital remboursé est fixe, tandis que les intérêts diminuent au fil des remboursements. La mensualité totale diminue progressivement.
- Annuités Constantes (ou Mensualités Constantes) : La mensualité reste la même tout au long du prêt. La part d’intérêt diminue tandis que l’amortissement augmente au fil du temps.
- Emprunt In Fine : L’emprunteur ne paie que les intérêts pendant la durée du prêt et rembourse le capital en une seule fois à l’échéance.
4. Calcul de la Mensualité pour un Emprunt à Annuités Constantes
La formule pour calculer la mensualité d’un prêt à annuités constantes est :
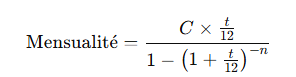
Où :
- CCC = Capital emprunté,
- ttt = Taux d’intérêt annuel,
- nnn = Nombre total de mensualités.
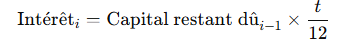
Calculer les Intérêts pour chaque Période :
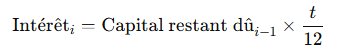
Calculer l’Amortissement :
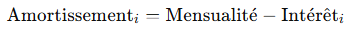
Mettre à Jour le Capital Restant Dû :
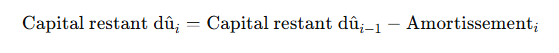
6. Exemple de Tableau d’Amortissement
Données de l’emprunt :
- Montant de l’emprunt : 10 000 €
- Taux d’intérêt annuel : 5 %
- Durée : 5 ans (60 mois)
- Mensualité calculée : 188,71 €
| Mois | Mensualité (€) | Intérêt (€) | Amortissement (€) | Capital restant dû (€) |
|---|---|---|---|---|
| 1 | 188.71 | 41.67 | 147.04 | 9 852.96 |
| 2 | 188.71 | 41.05 | 147.66 | 9 705.30 |
| 3 | 188.71 | 40.44 | 148.27 | 9 557.02 |
| … | … | … | … | … |
| 60 | 188.71 | 0.78 | 187.93 | 0 |
Remarque : Au fil des mois, la part des intérêts diminue et la part d’amortissement augmente, tout en gardant la mensualité constante.
7. Analyse et Utilité du Tableau d’Amortissement
- Suivi du Remboursement : Permet de voir la part du capital remboursé et le capital restant dû à chaque période.
- Calcul du Coût Total du Crédit : En additionnant toutes les mensualités, on obtient le coût total du crédit (capital + intérêts).
- Planification Financière : Aide l’emprunteur à planifier ses finances, notamment en cas de remboursement anticipé.
8. Cas Particuliers à Prendre en Compte
- Remboursement Anticipé : Si l’emprunteur rembourse partiellement ou totalement le capital avant la fin du terme, le tableau doit être ajusté en conséquence.
- Changement de Taux : En cas de taux variable, le calcul des mensualités et des intérêts doit être adapté à chaque période de variation.
- Période de Différé : Dans certains prêts, les premiers mois peuvent être exempts de remboursement de capital (différé total ou partiel).
9. Résumé des Avantages et Inconvénients
| Avantages | Inconvénients |
|---|---|
| Suivi détaillé du prêt | Les calculs peuvent être complexes |
| Visualisation des intérêts payés | Peu flexible pour les taux variables |
| Facilité de gestion financière | Ajustements nécessaires en cas de variation |
10. Conclusion
Le tableau d’amortissement est un outil essentiel pour comprendre la répartition des paiements d’un emprunt, le coût des intérêts, et la progression du remboursement. Il aide les emprunteurs à mieux gérer leurs finances et à planifier leurs paiements sur le long terme.
Cette fiche pratique fournit une vue d’ensemble du fonctionnement du tableau d’amortissement, des formules de calcul, et des cas spécifiques à prendre en compte lors de la gestion d’un emprunt.
5. Étapes pour Créer un Tableau d’Amortissement
- Déterminer la Mensualité : Utiliser la formule ci-dessus pour un prêt à annuités constantes.
- Calculer les Intérêts pour chaque Période :
Voici un ensemble d’exercices corrigés sur le tableau d’amortissement d’un emprunt.
Exercice 1 : Calculer la Mensualité d’un Emprunt
Données :
- Montant de l’emprunt : 20 000 €
- Taux d’intérêt annuel : 4 %
- Durée de remboursement : 10 ans (120 mois)
Objectif : Calculer la mensualité pour un prêt à annuités constantes.
exercice:
données:
capital_emprunt: 20000
taux_annuel: 0.04
duree_mois: 120
formule:
mensualite: |
mensualite = (capital_emprunt * (taux_annuel / 12)) / (1 - (1 + (taux_annuel / 12))**(-duree_mois))
calcul:
mensualite: 202.49Solution :
La mensualité constante pour cet emprunt est de 202,49 €.
Exercice 2 : Calculer les Intérêts, Amortissement et Capital Restant Dû au Premier Mois
Données :
- Montant de l’emprunt : 15 000 €
- Taux d’intérêt annuel : 5 %
- Durée de remboursement : 5 ans (60 mois)
- Mensualité (calculée précédemment) : 283,07 €
Objectif : Calculer les intérêts, l’amortissement, et le capital restant dû au premier mois.
exercice:
données:
capital_initial: 15000
taux_annuel: 0.05
mensualite: 283.07
formules:
interet_premier_mois: |
interet = capital_initial * (taux_annuel / 12)
amortissement_premier_mois: |
amortissement = mensualite - interet
capital_restant_du_premier_mois: |
capital_restant_du = capital_initial - amortissement
calculs:
interet: 62.50
amortissement: 220.57
capital_restant_du: 14779.43Solution :
- Intérêts du premier mois : 62,50 €
- Amortissement du premier mois : 220,57 €
- Capital restant dû après le premier mois : 14 779,43 €
Exercice 3 : Compléter le Tableau d’Amortissement pour les Trois Premiers Mois
Données :
- Montant de l’emprunt : 12 000 €
- Taux d’intérêt annuel : 3 %
- Durée de remboursement : 3 ans (36 mois)
- Mensualité calculée : 349,79 €
Objectif : Compléter les intérêts, amortissements, et capital restant dû pour les trois premiers mois.
exercice:
données:
capital_initial: 12000
taux_annuel: 0.03
mensualite: 349.79
formules:
interet: |
interet_mois = capital_restant_du_precedent * (taux_annuel / 12)
amortissement: |
amortissement_mois = mensualite - interet_mois
capital_restant_du: |
capital_restant_du_mois = capital_restant_du_precedent - amortissement_mois
calculs:
mois_1:
interet: 30.00
amortissement: 319.79
capital_restant_du: 11680.21
mois_2:
interet: 29.20
amortissement: 320.59
capital_restant_du: 11359.62
mois_3:
interet: 28.40
amortissement: 321.39
capital_restant_du: 11038.23Solution :
| Mois | Mensualité (€) | Intérêt (€) | Amortissement (€) | Capital restant dû (€) |
|---|---|---|---|---|
| 1 | 349.79 | 30.00 | 319.79 | 11 680.21 |
| 2 | 349.79 | 29.20 | 320.59 | 11 359.62 |
| 3 | 349.79 | 28.40 | 321.39 | 11 038.23 |
Exercice 4 : Calcul de la Dernière Mensualité et Capital Restant Dû
Données :
- Montant de l’emprunt : 5 000 €
- Taux d’intérêt annuel : 6 %
- Durée de remboursement : 2 ans (24 mois)
- Mensualité (calculée) : 221.60 €
Objectif : Calculer les intérêts, l’amortissement, et le capital restant dû au dernier mois.
exercice:
données:
capital_initial: 5000
taux_annuel: 0.06
mensualite: 221.60
duree_mois: 24
formules:
interet_dernier_mois: |
interet = capital_restant_du_precedent * (taux_annuel / 12)
amortissement_dernier_mois: |
amortissement = mensualite - interet
capital_restant_du_dernier_mois: |
capital_restant_du = capital_restant_du_precedent - amortissement
calcul_dernier_mois:
interet: 1.11
amortissement: 220.49
capital_restant_du: 0Solution :
- Intérêt du dernier mois : 1,11 €
- Amortissement du dernier mois : 220,49 €
- Capital restant dû après la dernière mensualité : 0 € (prêt entièrement remboursé)
Ces exercices corrigés permettent de se familiariser avec les calculs nécessaires pour remplir un tableau d’amortissement et suivre l’évolution des intérêts, de l’amortissement, et du capital restant dû sur la durée d’un prêt.
Voici une série d’exercices corrigés avec des cas particuliers pour le tableau d’amortissement d’emprunt. Ces exercices comprennent des cas de taux variable, de remboursement anticipé, et d’emprunt à amortissement in fine.
Exercice 1 : Emprunt avec Taux Variable
Données :
- Montant de l’emprunt : 25 000 €
- Durée de remboursement : 5 ans (60 mois)
- Taux d’intérêt annuel initial : 3 % les deux premières années, puis 4 % pour les trois dernières années
Objectif : Calculer la mensualité pour chaque période et établir le tableau d’amortissement des trois premières périodes pour le taux initial, puis la première période après le changement de taux.
exercice:
cas: Taux variable
données:
capital_emprunt: 25000
taux_initial: 0.03
taux_apres_2_ans: 0.04
duree_mois: 60
formules:
mensualite_avec_taux_initial: |
mensualite = (capital_emprunt * (taux_initial / 12)) / (1 - (1 + (taux_initial / 12))**(-duree_mois))
mensualite_avec_taux_nouveau: |
mensualite = (capital_restant_du * (taux_apres_2_ans / 12)) / (1 - (1 + (taux_apres_2_ans / 12))**(-reste_duree_mois))
calcul:
mensualite_taux_initial: 449.22
mensualite_taux_nouveau: 461.79Solution :
- Mensualité avec taux initial (3 %) : 449,22 €
- Mensualité après changement de taux (4 %) pour le capital restant dû : 461,79 €
| Mois | Mensualité (€) | Intérêt (€) | Amortissement (€) | Capital restant dû (€) |
|---|---|---|---|---|
| 1 | 449.22 | 62.50 | 386.72 | 24 613.28 |
| 2 | 449.22 | 61.53 | 387.69 | 24 225.59 |
| 3 | 449.22 | 60.56 | 388.66 | 23 836.93 |
| … | … | … | … | … |
| 25 | 461.79 | 78.45 | 383.34 | 15 072.20 |
Remarque : Ce tableau prend en compte le changement de taux après 24 mois, entraînant une légère augmentation de la mensualité pour le reste de la période.
Exercice 2 : Remboursement Anticipé Partiel
Données :
- Montant de l’emprunt : 30 000 €
- Taux d’intérêt annuel : 4 %
- Durée de remboursement : 10 ans (120 mois)
- Mensualité initiale (calculée) : 304.16 €
- Remboursement anticipé de 5 000 € au 24e mois
Objectif : Calculer la mensualité recalculée après le remboursement anticipé.
exercice:
cas: Remboursement anticipé
données:
capital_emprunt: 30000
remboursement_anticipé: 5000
taux_annuel: 0.04
duree_mois: 120
mensualite_initiale: 304.16
formules:
capital_restant_du_apres_24_mois: |
capital_restant_du = capital_initial - somme_amortissements_24_mois - remboursement_anticipé
nouvelle_mensualite: |
nouvelle_mensualite = (capital_restant_du * (taux_annuel / 12)) / (1 - (1 + (taux_annuel / 12))**(-reste_duree_mois))
calculs:
mensualite_initiale: 304.16
capital_restant_du_apres_24_mois: 20263.45
nouvelle_mensualite: 226.56Solution :
- Mensualité initiale : 304,16 €
- Capital restant dû après remboursement anticipé : 20 263,45 €
- Nouvelle mensualité après remboursement anticipé : 226,56 €
| Mois | Mensualité (€) | Intérêt (€) | Amortissement (€) | Capital restant dû (€) |
|---|---|---|---|---|
| 24 | 304.16 | 59.85 | 244.31 | 20 263.45 |
| 25 | 226.56 | 67.54 | 159.02 | 20 104.43 |
Remarque : Après le remboursement anticipé, la mensualité diminue, réduisant le coût global du crédit.
Exercice 3 : Emprunt In Fine
Données :
- Montant de l’emprunt : 50 000 €
- Taux d’intérêt annuel : 5 %
- Durée de remboursement : 5 ans (60 mois)
- Emprunt in fine : remboursement intégral du capital à la fin
Objectif : Calculer les intérêts payés chaque mois et le montant total dû à la fin du prêt.
exercice:
cas: Emprunt in fine
données:
capital_emprunt: 50000
taux_annuel: 0.05
duree_mois: 60
formules:
interet_mensuel: |
interet = capital_emprunt * (taux_annuel / 12)
remboursement_final: |
remboursement_final = capital_emprunt + (interet_mensuel * duree_mois)
calculs:
interet_mensuel: 208.33
remboursement_final: 62500.00Solution :
- Intérêt mensuel constant : 208,33 €
- Remboursement final (capital + intérêts) : 62 500 €
| Mois | Intérêt (€) | Amortissement (€) | Capital restant dû (€) |
|---|---|---|---|
| 1 | 208.33 | 0.00 | 50 000.00 |
| 2 | 208.33 | 0.00 | 50 000.00 |
| … | … | … | … |
| 60 | 208.33 | 50 000.00 | 0 |
Remarque : Dans un emprunt in fine, seuls les intérêts sont payés chaque mois, et le capital est remboursé en une seule fois à la fin de la période.
Exercice 4 : Tableau d’Amortissement avec Période de Différé
Données :
- Montant de l’emprunt : 40 000 €
- Taux d’intérêt annuel : 3.5 %
- Durée de remboursement : 6 ans (72 mois)
- Différé total de 1 an (pas de capital ni intérêts remboursés durant les 12 premiers mois)
Objectif : Calculer le montant des mensualités après la période de différé.
exercice:
cas: Différé total
données:
capital_emprunt: 40000
taux_annuel: 0.035
duree_mois: 72
duree_differé: 12
formules:
mensualite_apres_differé: |
mensualite = (capital_emprunt * (taux_annuel / 12)) / (1 - (1 + (taux_annuel / 12))**(-(duree_mois - duree_differé)))
calcul:
mensualite_apres_differé: 656.25Solution :
- Mensualité après période de différé : 656,25 €
| Mois | Mensualité (€) | Intérêt (€) | Amortissement (€) | Capital restant dû (€) |
|---|---|---|---|---|
| 1-12 | 0.00 | 0.00 | 0.00 | 40 000.00 |
| 13 | 656.25 | 116.67 | 539.58 | 39 460.42 |
| 14 | 656.25 | 115.29 | 540.96 | 38 919.46 |
Remarque : Pendant la période de différé, aucun remboursement n’est effectué, mais les mensualités augmentent après cette période pour compenser le retard de remboursement du capital.
Ces exercices avec cas particuliers montrent comment adapter les calculs du tableau d’amortissement en fonction des situations spécifiques : taux variable, remboursement anticipé, emprunt in fine, et période de différé.