Régression linéaire dans Excel : Un Outil Essentiel pour l’Analyse des Données
Recommandés
Dans ce contexte, Excel, le logiciel de feuille de calcul largement utilisé, offre une solution accessible pour effectuer des analyses de régression linéaire, permettant ainsi aux utilisateurs de tirer des conclusions pertinentes à partir de leurs données.
Dans le monde des affaires, de la recherche scientifique et de nombreux autres domaines, l’analyse des données joue un rôle crucial dans la prise de décision éclairée. La régression linéaire est l’une des méthodes statistiques les plus fondamentales utilisées pour comprendre les relations entre les variables.
Utilité
La régression linéaire dans Excel permet aux utilisateurs de modéliser et de comprendre les relations entre une variable dépendante et une ou plusieurs variables indépendantes. Voici quelques-unes des utilisations courantes de cette technique :
- Prévision et prévision : En utilisant des données historiques, la régression linéaire peut aider à prédire les valeurs futures d’une variable dépendante.
- Identification des tendances : En analysant les coefficients de régression, il est possible de déterminer si une variable indépendante a une influence significative sur la variable dépendante.
- Analyse des relations : La régression linéaire peut révéler des relations complexes entre différentes variables, permettant ainsi de mieux comprendre les dynamiques sous-jacentes d’un phénomène.
Applications
La régression linéaire dans Excel trouve des applications dans divers domaines :
Finance
Dans le domaine financier, la régression linéaire peut être utilisée pour modéliser les relations entre les facteurs économiques tels que le taux d’intérêt, le PIB et les prix des actifs financiers.
Marketing
Les professionnels du marketing utilisent la régression linéaire pour analyser l’impact des dépenses publicitaires, des prix des produits et d’autres variables sur les ventes.
Sciences sociales
Les chercheurs en sciences sociales utilisent la régression linéaire pour étudier les relations entre les variables telles que le revenu, l’éducation et la santé.
Sciences naturelles
Les scientifiques utilisent la régression linéaire dans les sciences naturelles pour modéliser les relations entre les variables environnementales telles que la température, la précipitation et la croissance des plantes.
Applications
La régression linéaire dans Excel trouve des applications dans divers domaines :
Finance
Dans le domaine financier, les analystes peuvent utiliser la régression linéaire pour modéliser les relations entre les facteurs économiques tels que le taux d’intérêt, le PIB et les prix des actifs financiers.
Marketing
Les professionnels du marketing utilisent la régression linéaire pour analyser l’impact des dépenses publicitaires, des prix des produits et d’autres variables sur les ventes.
Sciences sociales
Les chercheurs en sciences sociales utilisent la régression linéaire pour étudier les relations entre les variables telles que le revenu, l’éducation et la santé.
Sciences naturelles
Dans les sciences naturelles, la régression linéaire est utilisée pour modéliser les relations entre les variables environnementales telles que la température, la précipitation et la croissance des plantes.
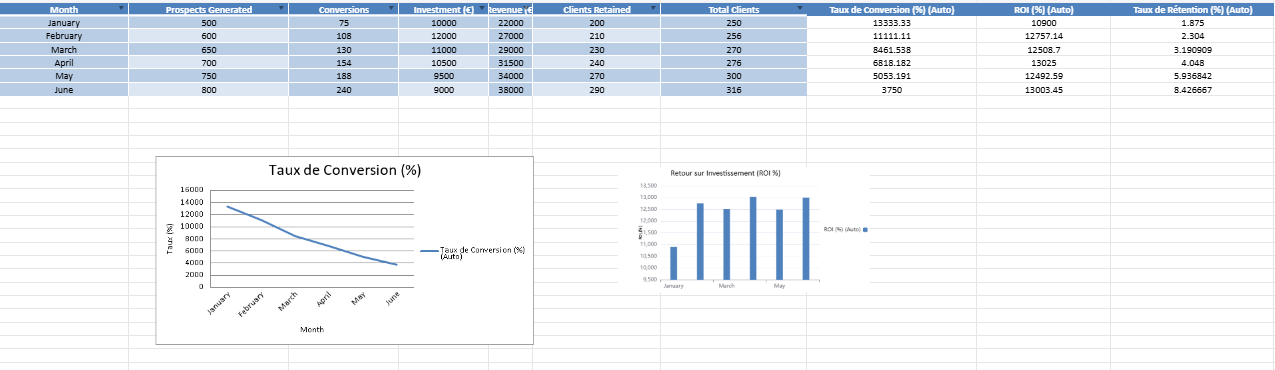
Tableau : Dépenses Publicitaires et Ventes de Produits Mensuelles
| Mois | Dépenses Publicitaires (en $) | Ventes de Produits |
|---|---|---|
| Jan | 5000 | 12000 |
| Fév | 6000 | 13000 |
| Mars | 5500 | 12500 |
| Avr | 7000 | 14000 |
| Mai | 8000 | 15000 |
| Juin | 7500 | 14500 |
| Juil | 9000 | 16000 |
| Août | 9500 | 16500 |
| Sept | 8500 | 15500 |
| Oct | 10000 | 17000 |
| Nov | 10500 | 17500 |
| Déc | 11000 | 18000 |
Ce tableau présente les données mensuelles sur les dépenses publicitaires et les ventes de produits pour une entreprise donnée sur une année. Les dépenses publicitaires sont en dollars ($) et les ventes de produits sont également en dollars ($).
{pratique} 🔍
Pour créer un modèle de régression linéaire dans Excel, vous pouvez utiliser l’outil d’analyse des données ou la fonction DROITEREG. Voici les étapes pour chacune des méthodes :
Utilisation de l’outil d’analyse des données
- Activer l’outil d’analyse : Si l’outil d’analyse n’est pas déjà activé, allez dans
Fichier>Options>Compléments. Dans le bas, choisissezCompléments Excelet cliquez surAtteindre. CochezOutils d’analysepuisOK. - Sélectionnez l’outil d’analyse : Allez dans
Données>Analyse des données. Si vous ne voyez pasAnalyse des données, assurez-vous que le complément est bien activé. - Choisissez
Régression: Dans la fenêtre d’analyse des données, sélectionnezRégressionet cliquez surOK. - Spécifiez les données d’entrée :
- Pour la
Plage Y, sélectionnez votre variable dépendante (la variable que vous essayez de prédire). - Pour la
Plage X, sélectionnez vos variables indépendantes (les variables prédictives).
- Pour la
- Configurer les options : Choisissez où vous souhaitez que la sortie soit générée (nouvelle feuille ou plage spécifique) et sélectionnez les options souhaitées comme les résidus.
- Exécution : Cliquez sur
OKpour exécuter l’analyse.
Utilisation de la fonction DROITEREG
Si vous souhaitez obtenir simplement l’équation de la droite de régression, vous pouvez utiliser la fonction DROITEREG.
- Syntaxe :
=DROITEREG(y; x; const; stats)yest la plage de données de votre variable dépendante.xest la plage de données de vos variables indépendantes.constspécifie si vous souhaitez forcer l’ordonnée à l’origine à passer par zéro (FAUX) ou non (VRAI).statsrenvoie des statistiques supplémentaires si mis àVRAI.
Exemple : Si vous avez vos valeurs Y en A1:A10 et vos valeurs X en B1:B10, pour obtenir l’équation de la droite, vous pouvez entrer la formule suivante dans deux cellules adjacentes pour obtenir la pente et l’ordonnée à l’origine de la régression linéaire : =DROITEREG(A1:A10;B1:B10;VRAI)
Ces méthodes vous permettent de construire et analyser un modèle de régression linéaire dans Excel, vous donnant une compréhension claire de la relation entre vos variables.
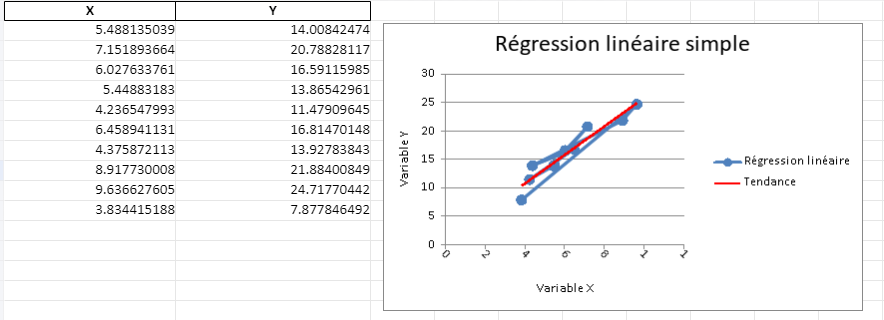
Conclusion
La régression linéaire dans Excel offre une méthode puissante et accessible pour analyser les relations entre les variables dans divers domaines. Que ce soit pour prédire les tendances financières, comprendre les comportements des consommateurs ou étudier les phénomènes naturels, cette technique permet aux utilisateurs de tirer des insights significatifs à partir de leurs données, contribuant ainsi à des prises de décision éclairées et à des avancées dans la recherche.