Exercices corrigés sur la gestion de projet – Analyse PERT
Recommandés
L’analyse PERT (Program Evaluation and Review Technique) est une méthode utilisée pour planifier et contrôler les projets. Elle se base sur l’estimation de la durée des activités, permettant de calculer la durée totale du projet en prenant en compte les incertitudes. Voici des exercices corrigés pour aider à comprendre et appliquer l’analyse PERT dans la gestion de projet.
Exercice 1: Calcul du temps moyen d’une activité
Situation :
Un projet comporte une tâche pour laquelle les durées optimiste, la plus probable et pessimiste ont été estimées comme suit :
- Durée optimiste : 4 jours
- Durée la plus probable : 6 jours
- Durée pessimiste : 10 jours
Question :
Calculez la durée moyenne (ou espérée) de l’activité en utilisant la formule PERT.
Formule PERT :
La durée estimée (TE) d’une activité dans la méthode PERT se calcule selon la formule :
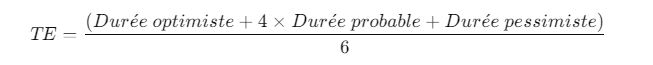
Données :
- (O = 4)
- (M = 6)
- (P = 10)
Résolution :
optimiste: 4
probable: 6
pessimiste: 10
temps_moyen: (optimiste + 4 * probable + pessimiste) / 6- Durée moyenne (TE) : 6,33 jours
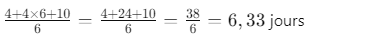
Conclusion : La durée moyenne pour cette activité est 6,33 jours.
Exercice 2: Identification du chemin critique
Situation :
Un projet a plusieurs tâches avec les durées moyennes suivantes (calculées à partir de PERT) :
- Tâche A (début du projet) : 4 jours
- Tâche B : 5 jours (dépend de la fin de A)
- Tâche C : 7 jours (dépend de la fin de A)
- Tâche D : 2 jours (dépend de la fin de B)
- Tâche E : 3 jours (dépend de la fin de C et D)
Question :
Identifiez le chemin critique du projet et la durée totale.
Données :
- A -> B -> D -> E
- A -> C -> E
Résolution :
Calcul de la durée des chemins possibles :
- Chemin 1 : A -> B -> D -> E = 4 + 5 + 2 + 3 = 14 jours
- Chemin 2 : A -> C -> E = 4 + 7 + 3 = 14 jours
Chemin critique :
Le chemin critique est le plus long chemin dans le projet. Les deux chemins prennent 14 jours, donc les deux chemins sont critiques dans ce cas.
Conclusion :
Le chemin critique du projet est A -> B -> D -> E et A -> C -> E, avec une durée totale de 14 jours.
Exercice 3: Calcul de la variance et écart type d’une activité
Situation :
Pour une tâche, les estimations PERT sont les suivantes :
- Durée optimiste : 3 jours
- Durée la plus probable : 5 jours
- Durée pessimiste : 9 jours
Questions :
- Calculez la variance de la durée de cette activité.
- Calculez l’écart type de la durée de cette activité.
Formule pour la variance :

Formule pour l’écart type :
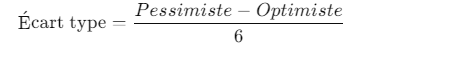
Données :
- (O = 3)
- (M = 5)
- (P = 9)
Résolution :
optimiste: 3
pessimiste: 9
variance: ((pessimiste - optimiste) / 6) ** 2
ecart_type: (pessimiste - optimiste) / 6- Variance : 1
- Écart type : 1
Conclusion :
- La variance de cette activité est de 1.
- L’écart type est de 1 jour.
Exercice 4: Probabilité de terminer un projet avant une date donnée
Situation :
La durée totale d’un projet est estimée à 40 jours. L’écart type total du projet (somme des écarts types de chaque tâche sur le chemin critique) est de 4 jours. Vous devez déterminer la probabilité que le projet soit terminé en 36 jours.
Question :
Quelle est la probabilité que le projet soit terminé en 36 jours ou moins ?
Formule de la valeur Z :

où :
- (D) est la durée cible (36 jours),
- (TE) est la durée moyenne du projet (40 jours),
- (sigma) est l’écart type total du projet (4 jours).
La valeur Z est ensuite utilisée pour déterminer la probabilité à partir d’une table de distribution normale.
Données :
- Durée moyenne (TE) = 40 jours
- Durée cible (D) = 36 jours
- Écart type ((sigma)) = 4 jours
Résolution :
duree_cible: 36
duree_moyenne: 40
ecart_type_total: 4
z: (duree_cible - duree_moyenne) / ecart_type_total- Valeur Z : -1
En consultant une table de distribution normale standard, la valeur Z = -1 correspond à une probabilité de 15,87 %.
Conclusion :
Il y a environ 15,87 % de chances que le projet soit terminé en 36 jours ou moins.
Exercice 5: Durée totale estimée d’un projet avec plusieurs tâches
Situation :
Un projet comporte trois tâches critiques avec les estimations PERT suivantes :
- Tâche A : optimiste = 2 jours, probable = 3 jours, pessimiste = 6 jours
- Tâche B : optimiste = 4 jours, probable = 5 jours, pessimiste = 7 jours
- Tâche C : optimiste = 3 jours, probable = 4 jours, pessimiste = 8 jours
Question :
Calculez la durée totale estimée du projet en additionnant les durées PERT des trois tâches.
Résolution :
Calcul des durées PERT pour chaque tâche :
- Tâche A : 3,33) jours
- Tâche B : 5,17 jours
- Tâche C : 4,5 jours
Durée totale estimée du projet :
Durée totale = 3,33 + 5,17 + 4,5 = 13 jours
Conclusion :
La durée totale estimée du projet est 13 jours.
Ces exercices corrigés en gestion de projet sur l’analyse PERT illustrent les concepts essentiels tels que le calcul de la durée moyenne des activités, la variance, l’écart type, et la probabilité de respecter des délais. Les calculs démontrent l’utilité de PERT dans la gestion de projets complexes avec des incertitudes sur les durées d’activités.