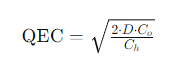Engrenage : cours de dessin industriel pratique pour débutant

Ce cours dessin industriel traite l’engrenage

Engrenages cylindriques droits

1. DEFINITIONS (PN.E.23.001 et 23.005).

Cylindre primitif de fonctionnement d’une roue d’engrenage: cylindre dette par L’axe instantané du mouvement relatif de la roue conjuguée par rapport à la roue considérée. (Les cylindres primitifs de deux roues d’engrenage à denture normale sont tangents l’un à l’autre suivant ure génératrice; leur diamètre est celui des roues de friction donnant le même rapport de vitesses.)

Cylindre de tête: cylindre contenant les sommets des dents.

Cylindre de pied : cylindre tangent au fond des entre-dents. Les diamètres de base de ces cylindres sont le diamètre primitif (d), le diamètre de tête (d,), le diamètre de pied(d,).

Module (m) : quotient du diamètre primitif d par le nombre de dents z.

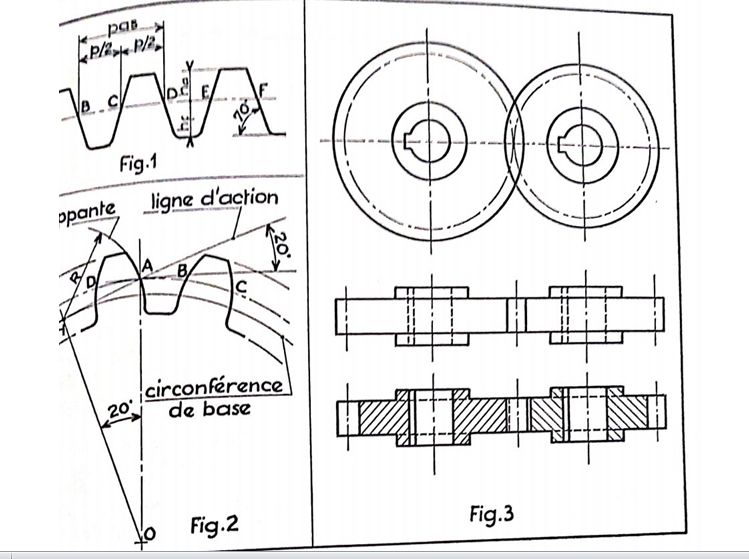
Pas (p):longueur de l’arc AB du cercle primitif compris entre deux profils homologues consécutifs (fig. 2) ; il est égal au produit du module par le nombre π ; en effet, la longueur de circonférence primitive est égale à n.d ou à p.z; doù p = π d/z = π.m.

Hauteur de la dent (h) : distance radiale entre le cercle de tête et le cercle de pied ; elle comprend la saillie (ha) et le creux (hz)(fig.2).

Largeur de denture (b) : largeur de la partie dentée d’une roue.

Ligne d’action (fig. 2) : normale commune à deux profils conjugués, en leur point de contact; dans un engrenage à développante, la ligne d’action est une droite fixe, tangente intérieurement aux deux cercles de base (fig. 2,page 113); les points de contact successifs de deux profils conjugués se déplacent sur la ligne d’action; la poussée d’une dent sur la dent de la roue conjuguée s’exerce suivant cette ligne.

Angle de pression (a):angle aigu compris entre le rayon du cercle primité ligne d’action fait un angle a avec la tangente nad cercle primitif.

NORMALISATION DES ENGRENAGES (E. 23.011)

Le but de cette normalisation est de rendre les engrenages interchangeables: deux roues normalisées de même module engrènent entre elles quels que soient leurs nombres de dents et leurs diamètres.

a) Tracé de référence : c’est la section droite de la crémaillère génératrice; ce tracé est à profil rectiligne (fig 1); il est caractérisé par :

Angle de pression de 20°;

Saillie égale au module;

Creux égal à 1,25 module;

Rayon de l’arrondi au fond des entre-dents : 0,4 module au maximum.

b) Profil des dents de la roue : c’est un arc de développante de cercle (voir p. 21). La denture est dite « normale » si la ligne de référence de la crémaillère est tangente au cylindre primitif de la roue, « déportée » si elle n’est pas tangente à ce cylindre.

Dimensions des dents de la denture normale (fig.2):

Saillie ha=module m

Creux h1=1,25m

c) Modules. La série des modules normalisés comprend une série principale (en caractères gras), une série secondaire, une série de valeurs exceptionnelles (entre parenthèses).

0,5-0,55-0,6-0,7-(0,75)-0,8-0,9-1-1,125-1,25-1,375-1,5-1,75 – 2 – 2,25 – 2,5 – 2,75 – 3 – (3,25)-3,5-(3,75)-4-4,5-5-5,5 – 6 – (6,5) -7-8-9-10 – 11 – 12 – 14- 16 – 18 – 20 – 22-25

CALCUL DES ELEMENTS DE LA DENTURE (denture nomale)

Données:

Calcul:

Saillie: ha=m.

Creux: hr=1,25 m.

Hauteur: h=ha+h1=2,25m.

Diamètre primitif : d = m.z.

Diamètre de tête :da=d+2m=m(z+2).

Diamètre de pied: dr=d-2,5m=m(z-2,5).

Pas:p=m.π.

Distance d’axes de deux roues en prise:

a=(m.z1/2)+(m.z2/2)=m(z1+Z2)/2.

Choix de la fraise. On utilise un jeu de huit fraises par module.

Au-dessus du module 10, on utilise fréquemment un jeu dequinze fraises par module

REPRESENTATION DES ENGRENAGES.

a)PRINCIPE DU TRACE DU PROFIL DES DENTS.

1. Crémaillère (fig. 1). Le profil est rectiligne, incliné à 70° (complément de l’angle de pression) ; d’où le tracé suivant :

-Tracer la ligne primitive, les lignes de tête et de pied ;

Porter des longueurs AB, BC, CD…, etc. = 1/2 pas ;

-Tracer par les points de division des droites inclinées à 70° par rapport à l’horizontale.

2. Roue dentée (fig. 2). Le profil est un arc de développante de cercle, obtenu en faisant rouler sans glisser la ligne d’action sur la circonférence de base; celle-ci est concentrique à la circonférence primitive et tangente à la ligne d’action.

D’où le tracé suivant :

– Tracer les circonférences primitives, de tête et de pied;

-Tracer la ligne d’action (angle de pression : 20°);.

-Abaisser la perpendiculaire OH sur la ligne d’action et tracer la circonférence de base, de centre O, de rayon OH.

Faire rouler la ligne d’action sur la circonference de base;le point

passant par A.

En dessin, pour représenter quelques dents,on peut remplacer Développante

REPRESENTATION SIMPLIFIEE (NF. E.04.113).

1. Vue de face. Ne pas représenter la denture, sauf cas exceptionnel (extrémité d’un secteur denté ou d’une crémaillère, par exemple); utiliser dans ce cas, de préférence, le trait continu fin. Représenter la roue comme une pièce pleine non dentée, avec tracé de la surface primitive en trait mixte fin (fig. 3). Ne pas représenter la surface de pied, sauf cas exceptionnel ; utiliser alors le trait continu fin.

2. Projection parallèle à l’axe. Ne pas représenter la denture. Représenter la roue comme une pièce pleine non dentée, avec tracé de la surface primitive en trait mixte fin (fig. 3). Ne pas représenter la surface de pied, sauf cas exceptionnel; utiliser alors le trait inter rompu court moyen (contour caché).

3. Coupe axiale. Faire la coupe comme s’il s’agissait d’une roue à denture droite ayant deux dents diamétralement opposées, représentées non coupées ; tracer la surface primitive en trait mixte fin (fig. 3).

4. Dessin de deux roues en prise. En vue de face et projection parallèle à l’axe, représenter chacune des roues comme si elle était seule. En coupe axiale, la dent de l’une des roues, arbitrairement choisie, est supposée cachée par celle de l’autre roue (fig. 3).

Dessins simplifiés et schémas

COTATION DE LA DENTURE: module, nombre de dents, diamètres primitif et de tête

Engrenages cylindriques hélicoïdaux

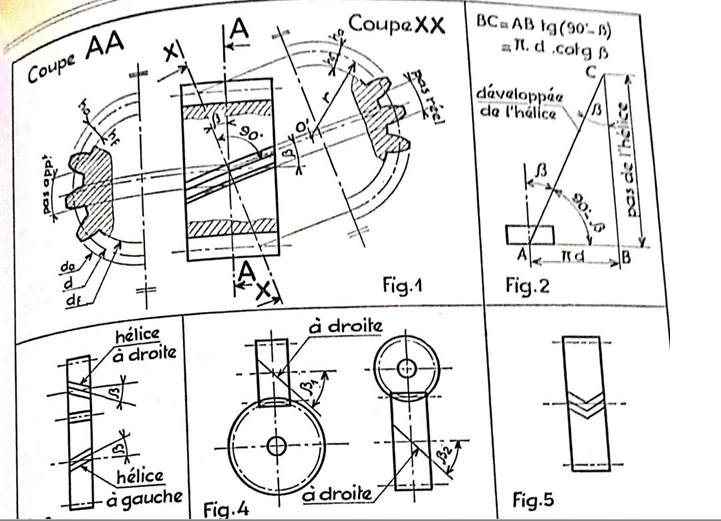
DEFINITIONS (PN.E 23.001 et 23.005).

Cette hélice est enroulée « à droite» ou «à gauche».

de l’angle β.

Primitif d par le nombre de dents z; on a donc les relations: xw=dəzxω=p

 le module correspondant est le module test

la relation: Pw=maxπ

Le pas réel étant la projection sur le plar xX du tos

apparent, on a : pa = pi x cos β et ma=m:xcos 3

 CALCUL DES ELEMENTS DE LA DENTURE.

Données. Module réel ma choisi dans la série des modules normalisés.

Nombre de dents z.

Angle d’hélice β.

Sens de l’hélice.

Calcul. Module apparent…….

m:=ma/cos β

Pas réel………….                              xw=d

Pas apparent….·····       P:= m:xπ

Saillie              h,=m

Creux …………..·     h1=1,25m。

Hauteur de la dent…..        h=2,25m

Diamètre primitif…… d=m:xz=mmxz/cos

Diametre de tête……        d1=d+2m

Diamètre de pied……       di=d-2,5m

Pas hélicoidal(fig.2).. BC=πd.cotg β

Distance d’axes…….. a=somme des rayons primitifs

Choix de la fraise. Dans le cas de taillage par fraise, celle-ci doit étre choisie d’après un nombre de dents fictif, correspondant au rayon de courbure! de la section du cylindre primitif, par un plan perpendiculaire a la denture (coupe XX, fig. 1).On démontre que zi=z/cos3 β.

RELATION ENTRE LES ELEMENTS DE DEUX ROUES EN PRISE.

a) Roues à axes parallèles (fig. 3).

Même pas réel, donc même module réel.

Même angle d’hélice (angle faible, voisin de 20°).

Même pas apparent, même module apparent.

Hélices de sens contraire.

b) Roues à axes orthogonaux (fig. 4).

Même pas réel, même module réel.

Inclinaisons complémentaires (β1+β2=90°); le plus souvent,

β1=β2=45°.

Hélices de même sens.

Pas apparents et modules apparents égaux si β1=β2.

Hélices de même sens.
Pas apparents et modules apparents égaux si β1=β2.
DESSIN. Mêmes conventions que pour les engrenages cylindriques droits. En projection parallèle à l’axe, indiquer, s’il y a lieu, le sens d’une denture hélicoidale ou en chevron par un signe rappelant la forme de cette denture (fig. 3 à 5):
Coter les diamètres primitifs, diamètres de tête, distance d’axes. Faire un tableau indiquant: module réel, module apparent, nombre de dents, angle et sens de l’hélice, pas de l’hélice.
D’engrenages à chevrons (fig. 5).

Engrenages coniques

DEFINITIONS (PN.E. 23.001 et 23.005).

et la longueur de génératrice R(fig. 1).

Cône de pied: cône tangent au fond des entre-dents; le demi-angle ou sommet est l’angle de pied δ4.

Largeur de denture b:largeur de la partie dentée de la roue, mesurée suivant une génératrice du cône primitif.

Module m:quotient du diamètre primitif par le nombre de dents; il est choisi dans la série des modules normalisés.

Hauteur de dent: distance entre le cercle de tête et le cercle de pied, mesurée suivant une génératrice du cône complémentaire; elle comprend la saillie ha et le creux hr; comme dans les engrenages cylindriques, on prend ha=m et hy= 1,25 m.

Angle de saillie θa: différence entre l’angle de tête et l’angle primitif.

Angle de creux 01 : différence entre l’angle primitif et l’angle de pied.

CALCUL DES ELEMENTS DE LA DENTURE (engrenages coniques à axes Perpendiculaires).

Données.

Module commun m (calculé en fonction de l’effort à transmettre).

Nombre de dents z1 et z2 (calculés en fonction du rapport des vitesses). Largeur de denture commune b.

Calcul.

Diamètres primitifs        d1=m.z1 et d2=m.Z2

Angles primitifs………… tg δ1=Z1/Z2 et tg δ2=Z2/Z1

d’où δ1 et δ2

Angle de saillie(commun)… tg 0a=m/R et R=d1/2 sin δ1;

Angle de creux(commun)…       d’où tg θa=2 sin δ1/z1

Angles de tête        tg 01=1,25m/R=2,5 sin δ1/Z1

Angles de pied………… δ1+θa et δa=δ2+0a

Diamètres de tête………. δ1-01 etδ1=82-0r                                                    

da = d1 +2m cos δ1 et d2 + 2 m cos δ2

DESSIN : Mêmes conventions que pour les engrenages cylindriques droits. et 122. Exemples de représentation, dessins simplifies et schémas

Tracé de deux roues en prise, représentées en coupe axiale (fig. 2). 1. Calcul des diamètres primitifs.

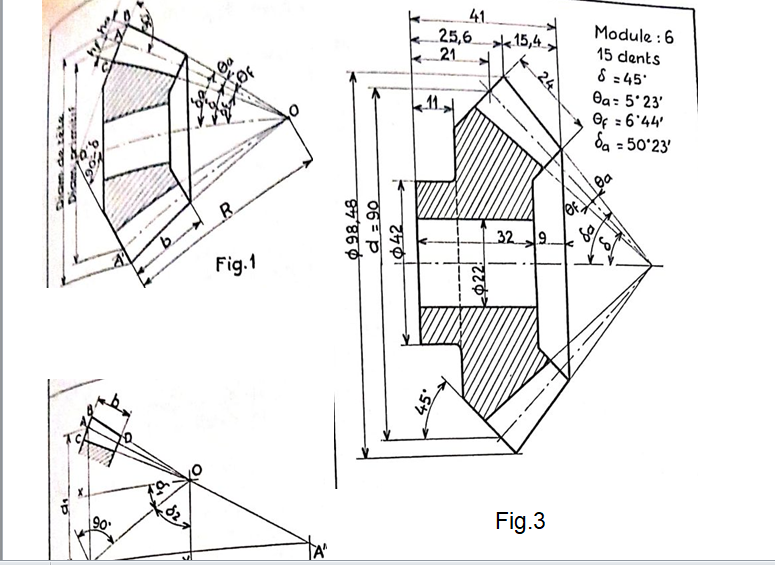
Tracé des cônes primitifs : tracer les axes, porter de partet d’autre les rayons primitifs ; tracer les génératrices OA, OA’, OA”; porter la longueur de denture AD.

3. Tracé des dents : élever la perpendiculaire en A à OA ; porter la saillie AB et le creux AC ; joindre OB et OC ; limiter les dents à la perpendiculaire en D à OA. Faire de même sur les génératrices OA’ et OA”.

4. Tracé de la jante, du moyeu, de la toile ou des bras.

Cotes nécessaires à la fabrication de la pièce brute et au tournage de

Cotes(fig.3).

La roue avant taillage. 2. Cotes des éléments de la denture, nécessaires au taillage des dents; ces cotes varient suivant la méthode de taillage employée, mais on indique généralement : module m, nombre de dents z, diamètre pri-mitif d, diamètre de tête da, largeur de denture b, angle primitif 8, angles de saillie 0a et de creux Or, angle de tête δa. Ces cotes peuvent être groupées dans un tableau. Les engrenages coniques de même module ne sont pas interchangeables comme les engrenages cylindriques; un pignon ne peut être utilisé qu’avec la roue avec laquelle il a été calculé et tracé

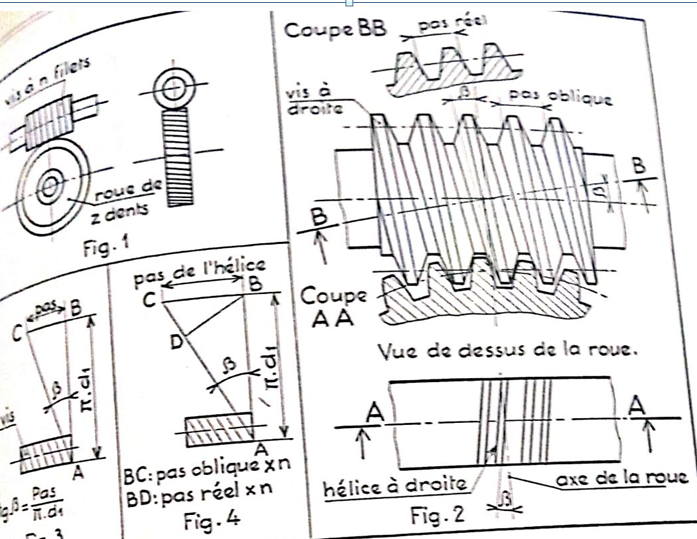
      Roue et vis sans fin

DEFINITIONS (non normalisées).
Réel de la vis.
données crémaillère plus allongée dont le module et le pas sont le module oblique et le pas oblique de la vis.
Distance entre deux spires du même filet = pas oblique X nombre de filets.
Roue. C’est une roue hélicoïdale, dont l’angle d’hélice est égal à l’inclinaison du filet de la vis par rapport à une section droite (angle β, fig. 2).

Le sens de l’hélice est le même sur la vis et sur la roue.

Le pas réel de la roue est égal au pas réel de la vis; il en est donc de même pour le module réel.

Le pas apparent et le module apparent de la roue sont égaux au pas oblique et au module oblique de la vis.

CALCUL DES ELEMENTS DE LA DENTURE.

Données. Vis: Nombre de filets n et sens de l’hélice

Module réel mn choisi dans la série des modules normalisés.

Diamètre primitif d1 choisi arbitrairement, de 10 à 15 m.

Roue : Nombre de dents z.

1″ cas : Vis à un seul filet. Dans ce cas, l’inclinaison du filet de la vis étant

Faible, le pas réel et le pas apparent sont sensiblement égaux ; si l’emploi de la roue et de la vis ne nécessite pas une grande précision, on peut confondre pratiquement le module réel et le module apparent. Par

exemple, pour une vis de diamètre primitif 35, de module réel 2,5, on

obtient β = 4° 5′ et le module apparent est 2,506.

D’où le calcul suivant :

Vis :Pas=mnXπ.

Inclinaison (fig.3):tg β=pas/π d1 = ma/d1, d’où β

Diamètre extérieur =d1+2mm.

Diamètre intérieur=d1-2,5 mm.

Roue:Angle d’hélice : β.

Module apparent: mt= mn.

Diamètre primitif:d2=mtxz=mnxz. etc

Vis : Inclinaison (fig. 4) : sin β=BD/BA=pas réel xn/π d1=

m.x n/d1.

Module oblique =m_/cos β. Pas réel=maxπ

Pas oblique =pas réel/cos β=maxπ/cos β.

Pas de l’hélice =pas oblique x n.

Diamètre extérieur =d1+2 ma.

Diamètre intérieur=d1-2,5 ma.

Roue: Angle d’hélice : β.

Module apparent = module oblique de la vis.

Diamètre primitif:d2 = m:xz=ma x z/cos β…etc.

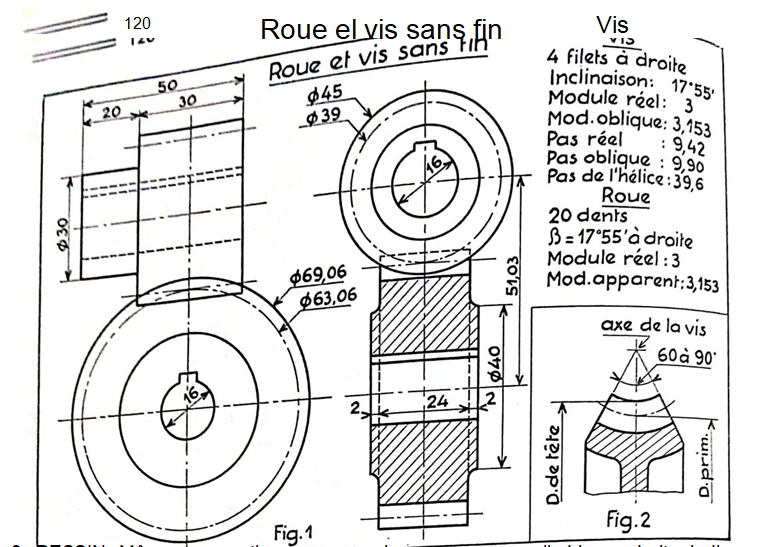
Exemple: Vis à 4 filets, d1 =39, ma = 3 ; roue de 20 dents.

On a:sin β=4 mn/39 = 12/39 = 0,30761 ; d’où β=17

Module oblique: ma/cos β=3/0,9515=3,153.

Pas oblique :3,153xπ=9,90.

Pas de l’hélice (nécessaire au tourneur) : 9,90 x4 = 39,6

etc.

Mêmes conventions que pour les engrenages cylindriques droits; indiquer éventuellement le sens de la denture hélicoïdale ou du filet de la vis par un signe rappelant la forme de cette denture. Sur le dessin de 2 roues en prise, si l’une des roues seulement est représentée en coupe, sa dent est supposée cachée par celle de la roue conjuguée, non coupée (fig. 1). Exemples de représentation, dessins simplifiés et schémas : voir pages 121 et 122.

Cotes. Vis et roue : diamètre primitif, de tête, de pied : distance d’axes.

Indications à porter sur le dessin:

Vis : nombre de filets, sens de l’hélice, inclinaison du filet, module réel et oblique, pas réel et oblique, pas de l’hélice.

Roue: nombre de dents, sens de l’hélice, angle d’hélice, module réel et apparent.

Exemple: voir fig.1.

4. ROUE ET VIS TANGENTE (fig. 2). Quand l’effort à transmettre est importante, on emploie souvent une roue creuse, enveloppant la vis suivant un arc de 60 à 90°; le contact entre la roue et la vis a lieu sur une plus grande longueur et l’usure est moins rapide. Le calcul est le même que pour une roue ordinaire.

Représentation des engrenages (NF.E.04.113)

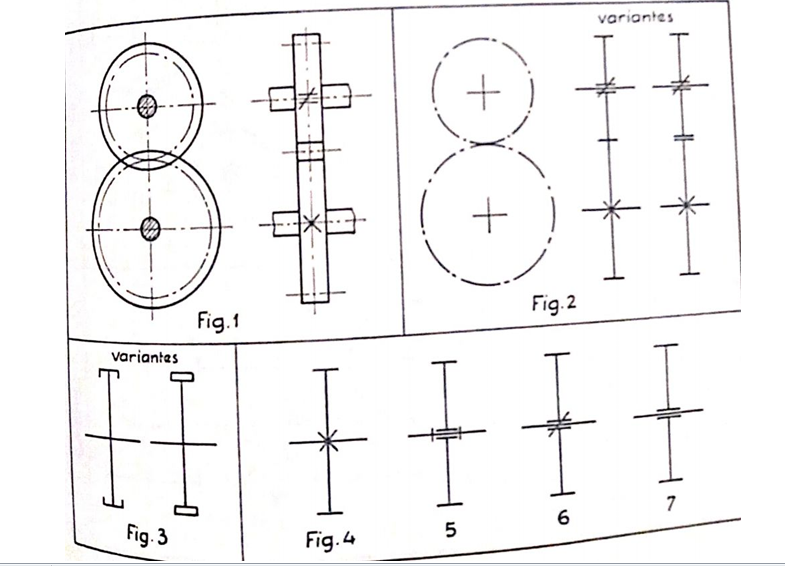
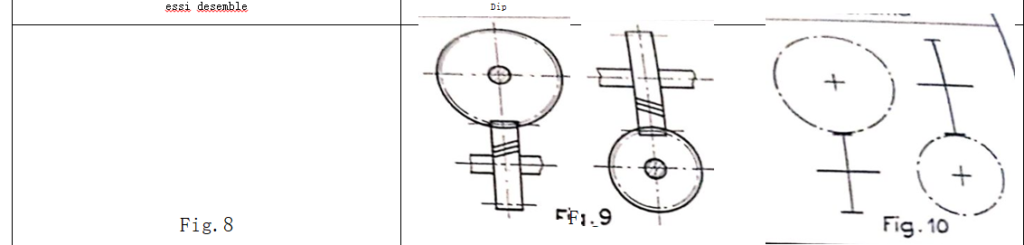
SCHEMAS (pour chaines cinématiques).

Représenter chaque roue par sa circonférence primitive, en trait mixte. Ex.: fig. 2, 10, 13, 16. Projection parallèle à l’axe : Représenter la roue par le contour apparent

Sa surface primitive, en trait continu (fig. 2).Faire une vue développée de la chaine cinématique. Représentation des roues de friction: voir fig.3

c Liaison avec l’axe. Liaison complète:fig.4;liberé en rotation:fig.5: liberté en translation : fig. 6 ; en rotation et translation :fig.7.

EXEMPLES DE REPRÉSENTATION