Cours et Exercices Corrigés : Maintenance Industrielle et Sûreté de Fonctionnement
Ce guide vise à structurer votre apprentissage autour des concepts clés de la maintenance industrielle et de la sûreté de fonctionnement. En suivant ce guide, vous pourrez :
- Comprendre les différents types de maintenance et leur application.
- Appréhender les méthodes d’analyse de fiabilité et de sûreté.
- Utiliser des outils et des modèles pour calculer et améliorer la fiabilité et la disponibilité des systèmes.
1. Comprendre la Maintenance Industrielle
1.1 Définitions
- Maintenance : Ensemble des actions destinées à maintenir ou à rétablir un bien dans un état spécifié (ex. norme AFNOR NF X 60-010).
- Préventive : Action visant à anticiper les défaillances.
- Corrective : Action mise en œuvre après une panne pour rétablir le fonctionnement.
1.2 Objectifs
- Sécurité : Assurer la protection des personnes et des équipements.
- Disponibilité : Maximiser la fiabilité et la maintenabilité des équipements.
- Durabilité : Prolonger la vie des équipements tout en minimisant les coûts.
2. Processus de Maintenance
2.1 Cycle de Vie de l’Équipement
- Le cycle de vie d’un matériel se divise en plusieurs phases :
- Conception : Inclut la prise en compte des besoins en maintenance.
- Fabrication : Assure la maintenabilité des équipements.
- Exploitation : Inclut la maintenance opérationnelle.
2.2 Types de Maintenance
- Maintenance Corrective : Se compose du dépannage (interventions temporaires) et de la réparation (interventions définitives).
- Maintenance Préventive : Prévue selon un calendrier (systématique) ou déclenchée par la surveillance de l’état des équipements (conditionnelle).
3. Stratégies de Maintenance
3.1 Choix d’une Politique de Maintenance
- Critères de choix : Type de défaillance, compétences du personnel, coûts de maintenance et organisation du travail.
- Méthodes de décision : Évaluer le coût des pannes, les options de surveillance et les impacts sur la sécurité.
3.2 Outils de Décision
- Diagrammes de décision : Utilisés pour déterminer les actions appropriées selon les coûts de pannes et la rentabilité des solutions proposées.
4. Fiabilité et Lois de Fiabilité
4.1 Concepts de Fiabilité
- Fiabilité (R(t)) : Probabilité qu’un système fonctionne sans panne sur une période donnée.
- Défiabilité (F(t)) : Complément de la fiabilité, représentant la probabilité de panne.
4.2 Lois de Fiabilité
- Loi Exponentielle : Modèle de défaillances aléatoires, utilisée lorsque le taux de défaillance est constant.
- Loi de Weibull : Modélise les trois phases de vie des équipements (jeunesse, maturité, vieillesse).
5. Méthodes d’Analyse de Fiabilité
5.1 Diagramme Bloc Fiabilité (RBD)
- Principe : Modéliser les composants d’un système sous forme de blocs pour évaluer la fiabilité globale.
- Configurations de Systèmes :
- Série : L’échec de n’importe quel composant entraîne l’échec du système.
- Parallèle : Le système fonctionne tant qu’au moins un composant fonctionne.
5.2 Arbre de Défaillance (Fault Tree)
- Objectif : Identifier et quantifier les combinaisons de défaillances conduisant à une panne.
- Étapes de Construction :
- Identifier l’événement indésirable (panne),
- Tracer les événements intermédiaires et de base,
- Utiliser des portes logiques (ET, OU).
5.3 Graphes de Markov
- Utilité : Modéliser les systèmes réparables en représentant les états de fonctionnement et de défaillance par des transitions.
- Applications : Utilisé pour calculer la fiabilité et la disponibilité des systèmes en fonction des taux de transition.
6. Concepts de Fiabilité, Maintenabilité et Disponibilité (FMD)
6.1 Fiabilité (MTBF)
- MTBF (Mean Time Between Failures) : Temps moyen entre deux défaillances consécutives.
6.2 Maintenabilité (MTTR)
- MTTR (Mean Time To Repair) : Temps moyen pour réparer une défaillance.
6.3 Disponibilité
- Calcul de la Disponibilité : D = MTBF / MTBF + MTTR
- Types de Disponibilité :
- Intrinsèque : Mesurée dans des conditions idéales de fonctionnement.
- Opérationnelle : Mesurée dans les conditions réelles d’exploitation.
7. Exercices et Applications Pratiques
7.1 Études de Cas et Simulations
- Logiciel GRIF : Utilisez le module “Reliability Block Diagram” pour modéliser les diagrammes de fiabilité.
- TP sur l’Arbre de Défaillance : Utilisez le module “Fault Tree” pour construire et analyser des arbres de défaillance en appliquant des distributions (exponentielle, Weibull).
7.2 Utilisation des Banques de Données de Fiabilité
- Données internes (fiches d’intervention, retour client) et externes (bases de données de fiabilité) pour modéliser la durée de vie et optimiser la maintenance préventive.
Résumé des Concepts Clés
- Une bonne stratégie de maintenance repose sur l’analyse des données de fiabilité, le choix d’une politique de maintenance adaptée et l’optimisation de la disponibilité.
Bonnes Pratiques
- Utiliser les lois de fiabilité pour ajuster les périodes de maintenance.
- Employer des outils d’analyse (RBD, arbres de défaillance) pour prédire les risques et réduire les coûts d’intervention.
Ce guide peut servir de base pour des sessions d’apprentissage interactives, de travaux pratiques, et d’évaluation pour approfondir la compréhension des concepts de maintenance et de fiabilité.
1. Fiabilité et Formules Essentielles
Définitions :
- Fiabilité (R(t)) : Probabilité qu’un système fonctionne sans défaillance pendant une durée ttt.
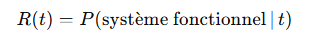
Défiabilité (F(t)) : Probabilité qu’un système tombe en panne avant le temps
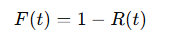
Taux de Défaillance (λ)
- Instantané : Le taux de défaillance à un instant ttt, noté λ(t)\lambda(t)λ(t), est donné par :
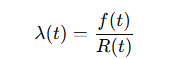
- où f(t)f(t)f(t) est la densité de probabilité des défaillances.
MTBF (Mean Time Between Failures) : Temps moyen entre défaillances pour des systèmes réparables.
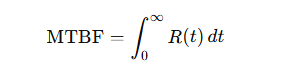
2. Lois de Fiabilité Principales et Graphiques
a) Loi Exponentielle
Utilisée lorsque le taux de défaillance est constant, typique pour la phase de maturité d’un équipement.
- Fonction de Fiabilité :
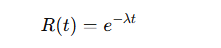
Densité de Probabilité :
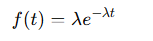
Fonction de Répartition (Défiabilité) :
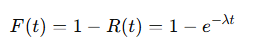
Graphique : La courbe de fiabilité R(t)R(t)R(t) décroît de manière exponentielle avec le temps ttt.
b) Loi Normale (Gaussienne)
Utilisée pour modéliser la phase de vieillissement, où les défaillances augmentent progressivement.
- Densité de Probabilité :
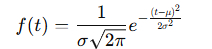
où μ\muμ est la moyenne et σ est l’écart type.
Fonction de Fiabilité :
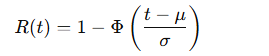
où Φ est la fonction de répartition cumulative de la loi normale.
Graphique : La courbe de fiabilité suit une distribution en cloche, avec une baisse marquée à partir d’un certain seuil de temps μ.
c) Loi de Weibull
Utilisée pour modéliser les trois phases de vie d’un équipement (jeunesse, maturité, vieillesse), grâce au paramètre de forme β qui détermine le type de défaillance.
- Fonction de Fiabilité :
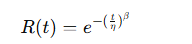
où η\etaη est le paramètre d’échelle, et β le paramètre de forme :
- β<1 : défaillances précoces
- β=1 : défaillances aléatoires (équivalent à la loi exponentielle)
- β>1 : défaillances en fin de vie (usure)
Densité de Probabilité :
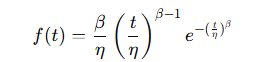
Graphique : La forme de la courbe dépend du paramètre β ; elle peut être décroissante, constante, ou croissante selon les phases d’usure du matériel.
Voici une série d’exercices sur la fiabilité et les lois de fiabilité avec des solutions.
Exercice 1 : Fiabilité d’un Système avec la Loi Exponentielle
Un composant électronique a un taux de défaillance constant de ( \lambda = 0.01 ) défaillances par heure. Calculer la probabilité que le composant fonctionne pendant 100 heures sans défaillance.
Solution
exercice_1:
donnée:
lambda: 0.01 # Taux de défaillance en défaillances par heure
t: 100 # Temps en heures
formule:
R_t: "exp(-lambda * t)" # Fonction de fiabilité pour la loi exponentielle
calcul:
R_t: 0.3679 # exp(-0.01 * 100) ≈ 0.3679
interprétation:
"La probabilité que le composant fonctionne sans défaillance pendant 100 heures est de 36.79%"Exercice 2 : Temps Moyen Entre Défaillances (MTBF)
Un équipement a un taux de défaillance ( \lambda = 0.02 ) défaillances par heure. Calculer le MTBF de l’équipement.
Solution
exercice_2:
donnée:
lambda: 0.02 # Taux de défaillance en défaillances par heure
formule:
MTBF: "1 / lambda" # Temps moyen entre défaillances pour la loi exponentielle
calcul:
MTBF: 50 # 1 / 0.02 = 50 heures
interprétation:
"Le temps moyen entre défaillances (MTBF) de l'équipement est de 50 heures."Exercice 3 : Loi Normale – Calcul de la Fiabilité
Un composant a une durée de vie suivant une loi normale avec une moyenne ( \mu = 500 ) heures et un écart type ( \sigma = 50 ) heures. Calculer la probabilité qu’il fonctionne au-delà de 550 heures.
Solution
exercice_3:
donnée:
mu: 500 # Moyenne en heures
sigma: 50 # Ecart type en heures
t: 550 # Durée en heures
formule:
Z: "(t - mu) / sigma" # Calcul du score Z pour la loi normale
P_T: "1 - Φ(Z)" # Fonction de fiabilité pour une loi normale
calcul:
Z: 1 # (550 - 500) / 50 = 1
P_T: 0.1587 # 1 - Φ(1) ≈ 0.1587
interprétation:
"La probabilité que le composant fonctionne au-delà de 550 heures est de 15.87%"Exercice 4 : Fiabilité d’un Système avec la Loi de Weibull
Un système a une durée de vie modélisée par une loi de Weibull avec un paramètre de forme ( \beta = 1.5 ) et un paramètre d’échelle ( \eta = 1000 ) heures. Calculer la probabilité que le système fonctionne au-delà de 800 heures.
Solution
exercice_4:
donnée:
beta: 1.5 # Paramètre de forme
eta: 1000 # Paramètre d'échelle en heures
t: 800 # Durée en heures
formule:
R_t: "exp(-(t / eta)^beta)" # Fonction de fiabilité pour la loi de Weibull
calcul:
R_t: 0.4724 # exp(-(800 / 1000)^1.5) ≈ 0.4724
interprétation:
"La probabilité que le système fonctionne au-delà de 800 heures est de 47.24%"Exercice 5 : Fiabilité de Systèmes en Série
Trois composants sont connectés en série avec des fiabilités respectives ( R_1 = 0.9 ), ( R_2 = 0.8 ), et ( R_3 = 0.95 ). Calculer la fiabilité du système.
Solution
exercice_5:
donnée:
R_1: 0.9 # Fiabilité du composant 1
R_2: 0.8 # Fiabilité du composant 2
R_3: 0.95 # Fiabilité du composant 3
formule:
R_systeme: "R_1 * R_2 * R_3" # Fiabilité totale pour des composants en série
calcul:
R_systeme: 0.684 # 0.9 * 0.8 * 0.95 ≈ 0.684
interprétation:
"La fiabilité du système composé des trois composants en série est de 68.4%"Ces exercices couvrent les concepts essentiels de la fiabilité et permettent de comprendre comment utiliser les lois de fiabilité dans des scénarios pratiques. Chaque exercice inclut les données, les formules, les calculs détaillés et une interprétation pour une meilleure compréhension.
Autres articles
