comment faire le calcul de l’écart type ( SD)étape par étape
Dans cet article, nous allons apprendre à calculer l’écart type “à la main”.
Fait intéressant, dans le monde réel, aucun statisticien ne calculerait jamais l’écart type à la main. Les calculs impliqués sont quelque peu complexes et le risque de se tromper est élevé. De plus, le calcul à la main est lent. Très lent. C’est pourquoi les statisticiens s’appuient sur des tableurs et des programmes informatiques pour calculer leurs chiffres.
Alors quel est l’intérêt de cet article ? Calcul de l’écart type
Pourquoi prenons-nous le temps d’apprendre un processus que les statisticiens n’utilisent pas réellement ? La réponse est qu’apprendre à faire les calculs à la main nous donnera un aperçu du fonctionnement réel de l’écart type. Cette perspicacité est précieuse. Au lieu de considérer l’écart type comme un nombre magique que nous donne notre tableur ou notre programme informatique, nous serons en mesure d’expliquer d’où vient ce nombre.
Aperçu de la façon de calculer l’écart type
La formule de l’écart type (SD) est : standard deviation= écart type
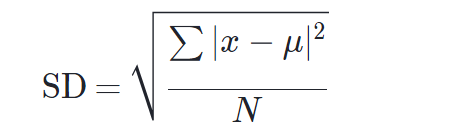
où \sum∑sum signifie “somme de”, xxx est une valeur dans l’ensemble de données, \muμmu est la moyenne de l’ensemble de données et NNN est le nombre de points de données dans la population.
La formule de l’écart type peut sembler déroutante, mais elle aura du sens une fois que nous l’aurons décomposée. Dans les prochaines sections, nous allons parcourir un exemple interactif étape par étape. Voici un aperçu rapide des étapes que nous sommes sur le point de suivre :
- Étape 1 : Trouvez la moyenne.
- Étape 2 : Pour chaque point de données, trouvez le carré de sa distance à la moyenne.
- Étape 3 : Additionnez les valeurs de l’étape 2.
- Étape 4 : Divisez par le nombre de points de données.
- Étape 5 : Prenez la racine carrée.
Une remarque importante
La formule ci-dessus sert à trouver l’écart type d’une population. Si vous avez affaire à un échantillon, vous voudrez utiliser une formule légèrement différente (ci-dessous), qui utilise n-1n−1n, moins, 1 au lieu de NNN. Le but de cet article, cependant, est de vous familiariser avec le processus de calcul de l’écart type, qui est fondamentalement le même quelle que soit la formule que vous utilisez.
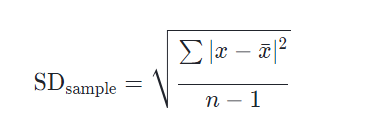
Exemple interactif étape par étape pour le calcul de l’écart type
Tout d’abord, nous avons besoin d’un ensemble de données avec lequel travailler. Choisissons quelque chose de petit pour ne pas être submergé par le nombre de points de données. En voici une bonne :
6, 2, 3, 16,2,3,1
Etape 1 : trouver
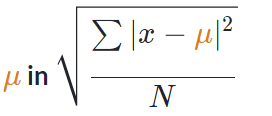
Dans cette étape, nous trouvons la moyenne de l’ensemble de données, qui est représentée par la variable.
Étape 2 : Trouver
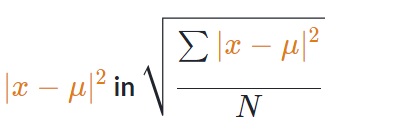
Dans cette étape, nous trouvons la distance entre chaque point de données et la moyenne (c’est-à-dire les écarts) et mettons au carré chacune de ces distances.
Par exemple, le premier point de données est 666 et la moyenne est 333, donc la distance entre eux est 333. La quadrature de cette distance nous donne 999.
Complétez le tableau ci-dessous :

Étape 3 : Trouver
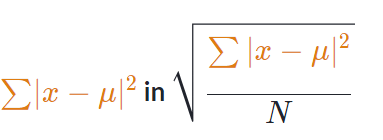
Le symbole \sum∑sum signifie “somme”, donc dans cette étape, nous additionnons les quatre valeurs que nous avons trouvées à l’étape 2.
Étape 4 : Trouver
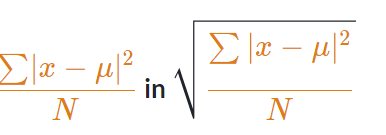
Dans cette étape, nous divisons notre résultat de l’étape 3 par la variable NNN, qui est le nombre de points de données.
Étape 5 : Trouver l’écart type
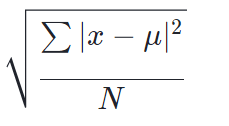
Nous avons presque fini ! Prenez simplement la racine carrée de la réponse de l’étape 4 et nous avons terminé.
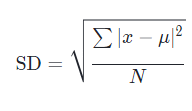
Résumé de ce que nous avons fait
Nous avons décomposé la formule en cinq étapes :
Étape 1 : Trouvez la moyenne
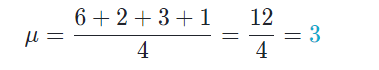
Étape 2 : Trouver le carré de la distance entre chaque point de données et la moyenne
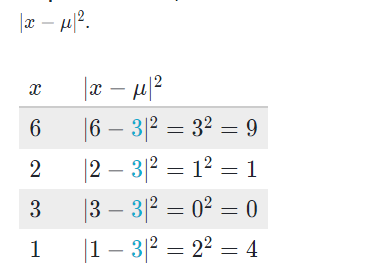
Étapes 3, 4 et 5 :
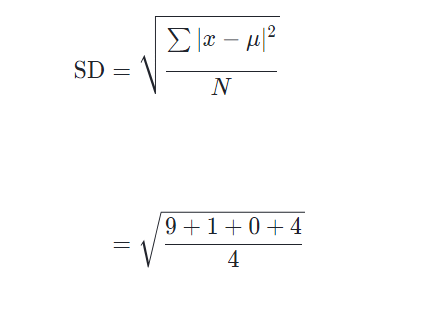

Essayez-le vous-même
Voici un rappel de la formule :
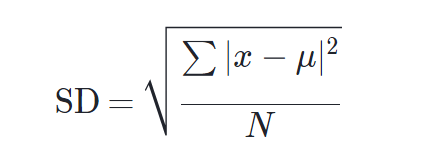
Et voici un ensemble de données :
1, 4, 7, 2,61,4,7,2,61, virgule, 4, virgule, 7, virgule, 2, virgule, 6
Trouvez l’écart type de l’ensemble de données.
Arrondissez votre réponse au centième près.