Le calcul du Coefficient de Variation (CV) dans Excel Un Outil Crucial pour l’Analyse de la Variabilité

Le coefficient de variation (CV) est un outil statistique essentiel utilisé dans divers domaines, de la finance à la biologie en passant par l’ingénierie et bien d’autres. Il mesure la dispersion relative des données par rapport à leur moyenne, fournissant ainsi une indication de la variabilité relative d’un ensemble de données. Le calcul du coefficient de variation est simple, mais sa signification peut être profonde dans l’interprétation des données. Cet article explore en détail la formule de calcul du coefficient de variation, son utilisation et son interprétation.

Formule de Calcul

Le coefficient de variation (CV) est défini comme le rapport de l’écart-type à la moyenne, exprimé en pourcentage. Mathématiquement, il est représenté comme suit :

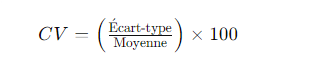
Où :

• Écart-type : mesure de la dispersion des valeurs dans un ensemble de données.
• Moyenne : valeur moyenne de l’ensemble de données.

Interprétation

Le coefficient de variation exprime la variabilité relative des données par rapport à leur moyenne. Un coefficient de variation plus élevé indique une plus grande dispersion des données par rapport à la moyenne, ce qui implique une plus grande incertitude ou une plus grande volatilité dans l’ensemble de données. D’autre part, un coefficient de variation plus faible suggère une dispersion plus faible des données autour de la moyenne, ce qui peut indiquer une plus grande stabilité ou précision dans les mesures.

Exemple Illustratif

Considérons deux ensembles de données :

1. Ensemble A : {10, 20, 30, 40, 50}
2. Ensemble B : {15, 25, 35, 45, 55}

Calculons le coefficient de variation pour ces ensembles de données :

Pour l’ensemble A :

Pour l’ensemble B :

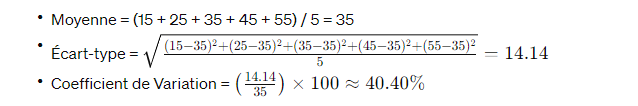
Dans cet exemple, bien que les ensembles de données aient le même écart-type, l’ensemble B a un coefficient de variation plus faible, ce qui suggère une dispersion relative moins importante par rapport à sa moyenne par rapport à l’ensemble A.

Applications Pratiques

Le coefficient de variation trouve des applications dans de nombreux domaines, notamment :

• Finance : pour évaluer le risque relatif d’un investissement.
• Biologie : pour mesurer la variabilité des caractéristiques biologiques.
• Ingénierie : pour évaluer la fiabilité et la variabilité des processus de fabrication.
• Économie : pour analyser la variabilité des données économiques telles que le PIB, l’inflation, etc.

Voici un modèle de tableau pour calculer le coefficient de variation (CV) :

Ensemble de Données	Moyenne	Écart-type	Coefficient de Variation
Données 1	…	…	…
Données 2	…	…	…
Données 3	…	…	…
…	…	…	…

Dans ce tableau :

• Ensemble de Données : Chaque ligne représente un ensemble de données spécifique pour lequel vous souhaitez calculer le coefficient de variation.
• Moyenne : Cette colonne est réservée pour inscrire la moyenne de chaque ensemble de données.
• Écart-type : Dans cette colonne, vous indiquez l’écart-type correspondant à chaque ensemble de données.
• Coefficient de Variation : Ici, vous pouvez calculer et inscrire le coefficient de variation pour chaque ensemble de données, en utilisant la formule précédemment mentionnée :

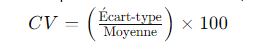
Pour chaque ensemble de données, vous remplissez cette colonne en effectuant ce calcul.

Ce modèle de tableau vous permet d’organiser les données de manière claire et de calculer efficacement les coefficients de variation pour plusieurs ensembles de données simultanément.

Pour créer un modèle de calcul du coefficient de variation (CV) dans Excel, vous pouvez suivre ces étapes. Le coefficient de variation est un indicateur statistique qui mesure la dispersion relative des données par rapport à la moyenne, et il est exprimé en pourcentage. Le CV est particulièrement utile pour comparer la variabilité entre des séries de données de différentes unités de mesure ou moyennes. La formule pour calculer le coefficient de variation est la suivante :

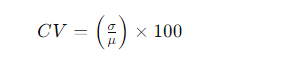
où (\sigma) est l’écart-type et (\mu) est la moyenne de l’ensemble de données.

Étapes pour Calculer le Coefficient de Variation dans Excel

1. Entrer les données : Commencez par entrer vos données dans une colonne d’une feuille Excel. Par exemple, si vous avez des données de vente mensuelles, vous pouvez les entrer de la cellule A2 à A13.
2. Calculer la moyenne : Dans une cellule vide, utilisez la fonction MOYENNE pour calculer la moyenne de vos données. Par exemple, si vos données sont en A2:A13, vous pouvez entrer la formule suivante dans la cellule B2 :

   =MOYENNE(A2:A13)

3. Calculer l’écart-type : Dans la cellule suivante (par exemple, B3), utilisez la fonction ECARTYPE.P pour les populations ou ECARTYPE.S pour les échantillons, afin de calculer l’écart-type de vos données. Pour une population :

   =ECARTYPE.P(A2:A13)

Pour un échantillon :

   =ECARTYPE.S(A2:A13)

4. Calculer le coefficient de variation : Dans une autre cellule (par exemple, B4), calculez le coefficient de variation en utilisant les résultats des étapes 2 et 3. La formule sera :

   =(B3/B2)*100

Ceci calcule le CV en pourcentage.

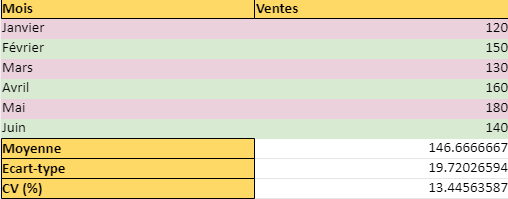
Exemple

Données
120
150
130
Moyenne	133,33
Ecart-type	15,28
CV (%)	11,46

Dans cet exemple, la moyenne est calculée dans la cellule B2, l’écart-type dans B3, et le coefficient de variation dans B4. Ce modèle simple peut être adapté et étendu selon vos besoins spécifiques.

Conclusion

Le coefficient de variation (CV) est un outil statistique puissant pour évaluer la variabilité relative des données. Sa capacité à normaliser la dispersion des données par rapport à leur moyenne en fait un outil précieux dans de nombreux domaines d’application. En comprenant et en utilisant le coefficient de variation de manière appropriée, les analystes peuvent obtenir des informations précieuses sur la nature et la stabilité des ensembles de données, ce qui peut éclairer la prise de décision dans divers contextes.